Parameter Integralrechnung Gleichung

Question

Welche Parabel f(x) =a*x²  halbiert die Fläche die der Graph von g(x) 2x-x² mit der x Achse einschließt

Zeigen sie dazu das die folgende Gleichung gelöst werden muss

Intervall (0| 2/a+1

A = [ g(x) -f(x) ] dx = 2/3

Mein Rechenweg:

x²- 1/3x³-1/3ax³  dann Intervalle einsetzen

Answer 1

Hallo Yasmin,

zuerst berechnest du die Nullstellen von g(x):

 2x - x²  = 0   ⇔  x * (2-x) = 0  ⇔  x = 0 oder x = 2 

dann musst du die Schnittstellen von f(x) und g(x)  bestimmen:

a * x² = 2x - x²

a *x² + x² - 2x = 0

(a + 1) * x² - 2x = 0

x * [ (a+1) * x - 2 ] = 0

1. Fall: a = -1 

f(x) = - x² verläuft unterhalb der x-Achse und kann deshalb die die im 1. Quadranten liegende Fläche, die g(x) mit der x-Achse einschließt, nicht halbieren.

1. Fall:  a+1 ≠ 0  ⇔ a ≠ -1

x = 0  oder  (a+1) * x - 2 = 0

x = 0 oder x = 2 / (a+1)  

Die Fläche A₁, d ie g(x) mit der x-Achse einschließt beträgt

 A₁  =  ₀ ∫²  (2x -x² ) dx  =  4/3 

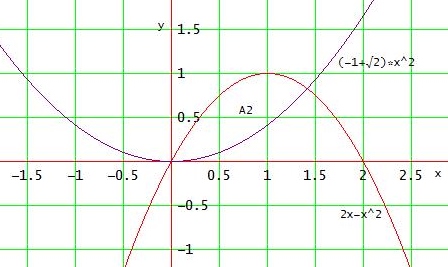
f(x) und g(x) schließen folgende Fäche A₂ ein:

A₂  =  ₀∫^2/(a+1) ( g(x) - f(x) )  dx  =  ₀∫^1/(a+1) (2x - x² - ax² )

        =   [ x² - 1/3 * x³ * (1+a) ] ]₀^2/(a+1)  =   4 / (3*(a + 1)²)

A₂ = 1/2 * A₁ = 2/3

 4 / (3*(a + 1)²)  = 2/ 3  ⇔ (a + 1)² = 2  ⇔ a + 1 = ± √2 ⇔ a = -1 ± √2

a = -1 - √2 < 0   entfällt aus dem gleichen Grund wie a = -1 (vgl. oben)

Also  :  a = -1 + √2  ;      f(x) = ( -1 + √2 ) * x² 

Gruß Wolfgang