2^y*3^0; 2^{y-1}*3^1; 2^{y-2}*3^2 und das ganze bis 2^1*3^{y-1} aufsummieren. Könnt ihr mir eine Formel angeben?

Question

Wollte fragen, ob es eine Summenformel für das, was unten steht gibt:

Also im Prinzip habe ich folgende Summanden:

2^y*3^0; 2^{y-1}*3^1; 2^{y-2}*3^2 und das ganze bis 2^1*3^{y-1}

Jetzt sollen alle Summanden addiert werden.

Gibt es jetzt eine Formel, die Summe in Abhängigkeit von y angibt?

Sorry, für diese komische Frage... ;)

Answer 1

Zuerst mal ist es wichtig zu sehen, dass du jeden Summanden $$2^{y-n}\cdot3^n$$ schreiben kannst als $$2^y\cdot(2^{-n}\cdot3^n)$$ und das ist dasselbe wie $$2^y\cdot\left(\frac32\right)^n$$.Das 2^y hängt nicht von n ab, und

$$\sum_{n=0}^{y-1}\left(\frac 32\right)^n=\frac{1-\left(\frac 32\right)^{(y-1)+1}}{1-\frac 32}=-2\left(1-\left(\frac 32\right)^y\right)=2\left(\left(\frac 32\right)^y-1\right).$$

Also ist deine Lösung:

$$2^{y+1}\left(\left(\frac 32\right)^y-1\right).$$

Comments

Ich verstehe noch nicht, warum die Lösung

2^{y+1}((3/2)^y-1) ist

und warum nicht

2((3/2)^y-1)

---

Oder doch, weil a_0=2^y ist, oder?

und weil 2^y*2=2^{y+1}

Aber danke für die Erklärung!

---

Genau deshalb.

Answer 2

2^y*3⁰; 2^y-1*3¹; 2^y-2*3² und das ganze bis 2¹*3^y-1

ist im Prinzip eine geometrische Folge mit q = 3/2 = 3*2^{-1} .

Nun suchst du bei den geometrischen Reihe nach der Formel für Partialsummen mit y Summanden. 

Damit kommst du zum Resultat. 

https://de.wikipedia.org/wiki/Geometrische_Reihe#Herleitung_der_Formel_f.C3.BCr_die_Partialsummen

Comments

Hab leider von dem Zeug noch nie was gehört... Kannst du's mir erklären?

---

Hab mich jetzt über Wikipedia etwas informiert...

Geht es um die Formel

s_n=a_0*(1-q^{n+1})/(1-q) ?

Dann hast du mir ja schon das q vorgegeben. Und n ist ja wahrscheinlich die Anzahl der summanden (also y). Dann fehlt mir ja nur noch a_0, was in meinem Fall 2^y ist, oder?

---

Die Formeln aus dem Link:

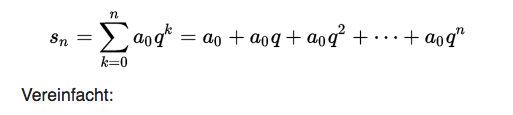
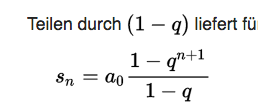
2^y*3⁰ + 2^y-1*3¹ +2^y-2*3² +.......+  2¹*3^y-1

= 2^y + 2^y*3/2 +2^y*3²/2^2 +.......+  2^y *3^y-1 / 2^{y^1} 

= 2^y  + 2^y * 3/2 +2^y * (3/2)^2 +.......+ 2^y* (3 / 2) ^{y-1} ) 

 q = 3/2 = 1.5 = 3*2^-1 , ao = 2^y,   n = y-1 . Nun Formel von oben benutzen

2^y*3⁰ + 2^y-1*3¹ +2^y-2*3² +.......+  2¹*3^y-1

= 2^y * ( 1 - 1.5^{y-1+1}) / ( 1 - 1.5) 

= 2^y * ( 1 - 1.5^{y}) / ( -0.5)   

= 2^y * (1.5^y - 1) / 0.5

= 2^{y+1} (1.5^y - 1) 

Bitte selber nachrechnen. 

---

Alles klar!

Danke für die Erklärung!