Ich habe eine Aufgabe bei der die 3.Wurzel einer komplexen Zahl gezogen werden soll.
Hier die Aufgabe:
Bestimmen Sie diejenige komplexe Zahl z, für die
z³=[√(3)+i]/2 ; Re(z)>0 ; Im(z)<0
gleichzeitig gilt.
Meine Lösung:
r=√[(√(3)/2)²+(1/2)²]=√[(3/4)+(1/4)]=1
φ=arctan((1/2)/(√(3)/2))=arctan(1/√3)=π/3
Mit der Formel n√z=n√(r) * e^{i*(φ+2πk)/n} mit k=0,1,...,n-1
folgt:
Z0=e^{i*π/9} Z1=e^{i*7π/9} Z2=e^{i*13π/9}
Wenn ich diese Ergebnisse in die komplexe Zahlenebene projeziere erkennt man dass keine der 3 Lösungen die Bedingungen Re(z)>0 und Im(z)<0 erfüllt.
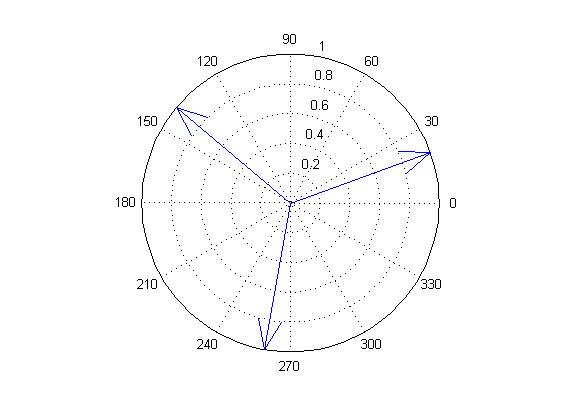
Jezt weiß ich leider nicht ob ich mich verrechnet habe oder vielleicht sonst einen Fehler gemacht habe, ob ich die Aufgabenstellung nicht richtig verstehe, oder ob ein Fehler in der Aufgabenstellung ist. Für eure Hilfe wäre ich wirklich sehr dankbar.
Gruß