Reihen konvergent, prüfen

Question

 

ich soll Reihen auf Konvergenz prüfen, komme jedoch nicht ganz weiter - wäre für einen übersichtlichen Lösungsweg sehr dankbar. (2te Frage diesmal mit Bild, da die Formatierung schief lief)

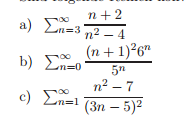
bei a.) habe ich soweit:

(n+1)+2/(n+1)^2-4/n+2/n^2-4 = (n+1)+2/(n+1)^2-4 * n^2-4/n+2

..komme leider nicht weiter

Comments

ich soll Reihen auf Konvergenz prüfen, komme jedoch nicht ganz weiter - wäre für einen übersichtlichen Lösungsweg sehr dankbar.
a.)
∞
∑      (n+2)/(n^2-4)
n=3
b.)∞
∑     (n+1)^2*6^n/5^n
n=0c.)∞
∑      n^2-7/(3n-5)^2 n=1 

---

bei a) gilt

(n + 2) / (n^2 - 4) = 1/(n - 2)

Answer 1

bei a) kannst du das Minorantenkriterium verwenden:

$$ \frac { n+2 }{ n^2-4 }>\frac { n }{ n^2-4 }>\frac { n }{ n^2 }=1/n $$

Die Reihe divergiert also (weil die harmonische Reihe divergiert).