Der Betrag von \(\vec{c}\) ist der Betrag von \(2\vec{a}-5\vec{b}\). Also kann man schreiben $$|\vec{c}|=|2\vec{a}-5\vec{b}|=\sqrt{(2\vec{a}-5\vec{b})^2}=\sqrt{4\vec{a}^2-20\vec{a}\vec{b}+25\vec{b}^2}$$
Wenn man weiß, das \(\vec{a}\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot \cos \alpha = 3\cdot 2 \cdot \frac{-1}{2}=-3\) ist, dann geht es weiter: $$=\sqrt{4\cdot3^2-20\cdot(-3)+25\cdot2^2}=\sqrt{196}=14$$
Anbei noch 'ne Skizze zur Kontrolle:
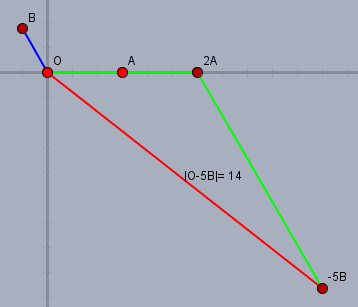
Den Winkel \(\beta\) zwischen \(\vec{a}\) und \(\vec{c}\) berechnet man aus \(\vec{a}\vec{c}=|\vec{a}|\cdot|\vec{c}|\cdot \cos\beta\). Daraus folgt: $$\cos \beta=\frac{\vec{a}\vec{c}}{|\vec{a}|\cdot|\vec{c}|}=\frac{\vec{a}(2\vec{a}-5\vec{b})}{3\cdot 14}=\frac{2\vec{a}^2-5\vec{a}\vec{b}}{42}=\frac{2\cdot3^2-5\cdot(-3)}{42}\\\approx 0,7857$$ daraus folgt $$\beta\approx38,21°$$
Gruß Werner