Ich nehme mal die normale Gleichung eines Rotationshyperboloids
x^2 / a^2 + y^2 / b^2 - z^2 / c^2 = 1
Da ich hier nur mal einen Querschnitt an der mit der xz Ebene betrachte ist y = 0
x^2 / a^2 - z^2 / c^2 = 1
Nun habe ich zwei Punktbedingungen
P(6/2 | 0)
P(12.75/2 | 7.5)
3^2/a^2 - 0^2/c^2 = 1
3^2/a^2 = 1
3^2 = a^2
a = 3
6.375^2/a^2 - 7.5^2/c^2 = 1
6.375^2/3^2 - 7.5^2/c^2 = 1
289/64 - 225/4/c^2 = 1
225/4/c^2 = -(1 - 289/64) = 225/64
225/4 = -(1 - 289/64) = 225/64*c^2
c^2 = (225/4) / (225/64) = 16
c = 4
Damit lautet die Gleichung des Rotationshyperboloids
x^2 / 9 - z^2 / 16 = 1
Skizze:
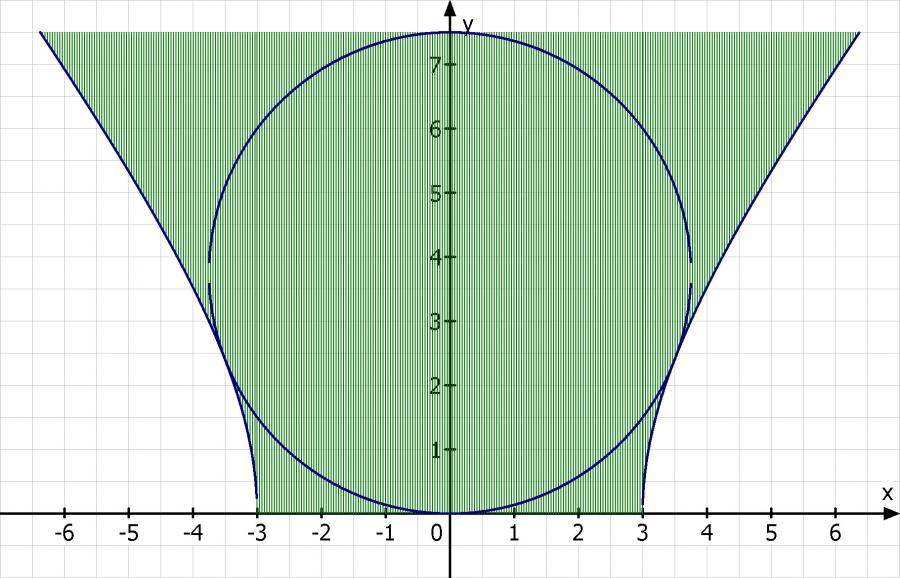
Rotationsintegral für das Volumen
x^2 / 9 - z^2 / 16 = 1
x = 3·√(z^2 + 16)/4
f(x) = 3·√(x^2 + 16)/4
Das Volumen wäre damit
∫ (0 bis 7.5) (pi·(3·√(x^2 + 16)/4)^2) dx
∫ (0 bis 7.5) (9/16·pi·(x^2 + 16)) dx
∫ (0 bis 7.5) (9/16·pi·x^2 + 9·pi) dx = 18765/128·pi = 460.6 cm^3
Nun wäre als erster Schritt zu klären ob ich die richtigen Annahmen getroffen habe und ob ich richtig gerechnet habe.
Sollte das der Fall sein wäre diesem Rotationshyperboloid eine Kugel einzubeschreiben. Ich würde da in etwa vorgehen das ich die Gleichung des Kreises in Abhängigkeit von r aufstelle. Dann soll der Kreis mit dem Graphen einen Berührpunkt haben. Also untersuche ich auf Schnittpunkte und nehme das r wo ich nur einen Gemeinsamen Punkt habe.
Willst du es zunächst mal nachrechnen und dann dich an dem Kreis probieren?