Inverse zur Lösung eines Linearen Gleichungssystems

Question

Die Inverse von      1     -1     -1        ist       -1     -1    1

                                   0      2       1                    2       2    -1 

                                   2        1       0                   -4    -3     2

Nutzen Sie diese zur Lösung des folgenden Systems linearer Gleichungen.

x - y - z = 0

2y  + z = 1

2x + y   = 2

Muss ich da auch eine Matrix zu dem LGS aufstellen und die mit der inversen multiplizieren?

Answer 1

nein - Du brauchst keine Matrix 'aufstellen', da die Matrix bereits gegeben ist. Das Gleichungssystem kannst Du auch schreiben: $$A\cdot\begin{pmatrix} x \\ y\\ z\end{pmatrix}=\begin{pmatrix} 0 \\ 1\\ 2\end{pmatrix}$$ Ist die Inverse von A bekannt, so kann man das ganze System rechts mit der Inversen multiplizieren $$ A^{-1}\cdot A\cdot\begin{pmatrix} x \\ y\\ z\end{pmatrix}=A^{-1} \cdot \begin{pmatrix} 0 \\ 1\\ 2\end{pmatrix}$$ und da \(A^{-1} \cdot A=1\) ist, erhält man $$\begin{pmatrix} x \\ y\\ z\end{pmatrix}=A^{-1} \cdot \begin{pmatrix} 0 \\ 1\\ 2\end{pmatrix}$$ Also

 

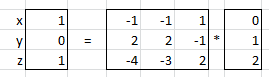
mache die Probe, und Du siehst, dass das Ergebnis stimmt.

Gruß Werner

Answer 2

Nein, die erste Matrix (sagen wir mal A )  ist doch die vom Gleichungssystem.

Das ist dann    A *  x =   b  

wobei x die Spalte


x
y
z



ist   und b der Vektor 

0
1
2

Also ist     x =  (Inverse von A) * b

Mutipliziere also die zweite Matrix mit dem Vektor b

und du hast die Ergebnisse für

x
y
z
.