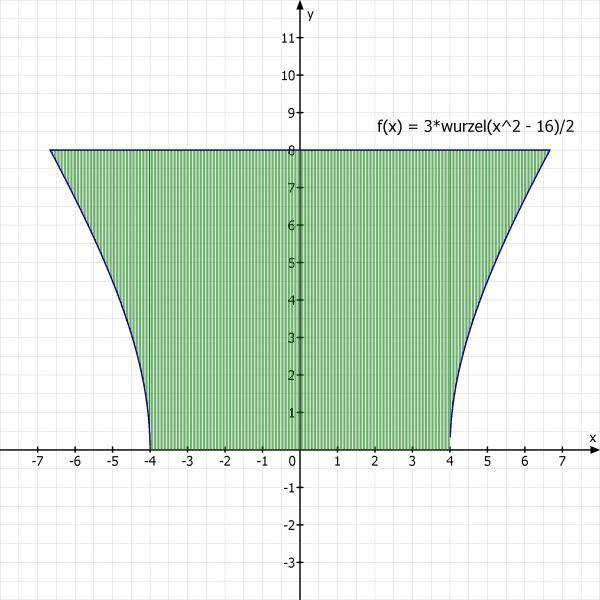
Der Hyperboloid
x^2/a - y^2/b = 1
Ich habe zwei Punktbedingungen (8/2, 0) und (40/6, 8)
(8/2)^2/a - 0^2/b = 1
16/a = 1
a = 16
(40/6)^2/16 - 8^2/b = 1
25/9 - 64/b = 1
b = 36
x^2/16 - y^2/36 = 1
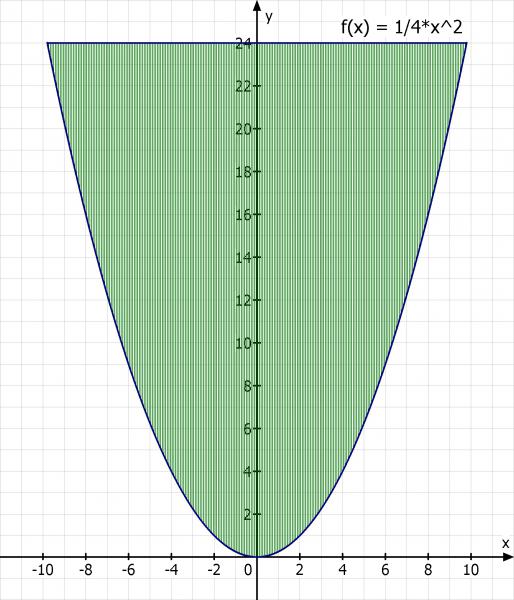
Der Paraboloid
y = a·x^2
Ich habe hier eine Punktbedingung (8√6/2, 24)
24 = a·(8·√6/2)^2
24 = 96·a
a = 1/4
y = 1/4·x^2