Die Aufgabe lautet: Welche Tangenten des Graphen G1 schließen mit der x Achse einen Winkel von 45 Grad ein ?
Der Winkel zwischen der x-Achse und einer weiteren Geraden
die die x-Achse schneidet wird normalerweise gegen den
Uhrzeigersinn angegeben.
0 - 90 - 180 - 270 Grad.
Wie im Koordinatensystem.
Man kann aber auch 315 ° = - 45 ° oder auch
abs 45 ° annehmen. Ich beschränke mich hier auf den 1.Fall
der Winkelhalbierenden des 1.Quadranten.
Es wurde nichts gegeben, außer die Funktion f(x) = 1/3xhoch3 - xhoch2 + x + 1/3
f ( x ) = 1/3 * x^3 - x^2 + x + 1/3
Die erste Ableitung lautet ja: f´(x) = xhoch2 - 2x + 1f ´( x ) = x^2 - 2 * x 1
Ich versuche einmal eine mathematischere Antwort
Für einen Berührpunkt ( hier die Funktion und die
Tangente ) gilt
f ( x ) = t ( x ) ( Schnittpunkt )
f ´( x ) = t ´( x ) ( die Steigung ist im Schnittpunkt gleich )
f ( x ) = 1/3 * x^3 - x^2 + x + 1/3
f ´( x ) = x^2 - 2 * x + 1
t ( x ) = m * x + b ( Geradengleichung )
t ´( x ) = m
m ist die Steigung der Tangente und beträgt
lauf Aufgabenstellung 1 ( 45 ° )
f ´( x ) = t ´( x ) ( die Steigung ist im Schnittpunkt gleich )
x^2 - 2 * x + 1 = 1
x^2 - 2 * x = 0
pq-Formel oder quadratische Ergänzung
oder hier einfacher Satz vom Nullprodukt
x^2 - 2 * x = 0
x * ( x - 2 ) = 0
x = 0
x = 2
f ( 0 ) = 1/3 * 0^3 - 0^2 + 0 + 1/3 = 1/3
Schnittpunkt ( 0 | 1/3 )
Für die Tangente gilt derselbe Punkt
y = 1 * 0 + b = 1/3
b = 1 /3
Tangentengleichung
t ( x ) = 1 * x + 1/3
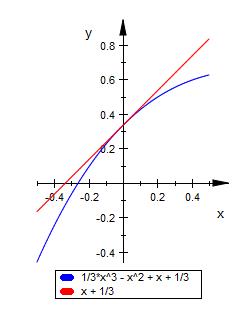
Und eine weitere Frage lautet: Wie kann man am Term von f´(x) erkennen, dass es keine Tangente mit negativem Steigungswinkel gibt.
f ´( x ) = x^2 - 2 * x + 1
ist die 2.binomische Formel
f ´( x ) = ( x - 1)^2
Die rechte Seite ist durch das Quadrat immer positiv
oder null.
Die Steigung der Funktion ist also immer
positiv oder 0.
Eine Tangente kann auch nur diese Steigung
haben also nicht -1.
Bei Bedarf nachfragen.
mfg Gold-und-Silber-lieb-ich sehr