LR-Zerlegung mit Totalpivotsuche

Question

 

 

ich bräuchte eure Hilfe! 

Ich habe die oben gegebene Matrix A, bei der ich die Totalpivotisierung (Zeilen- & Spaltentausch) anwenden möchte und stets das betragsgrößte Element als Pivot setzen will. 

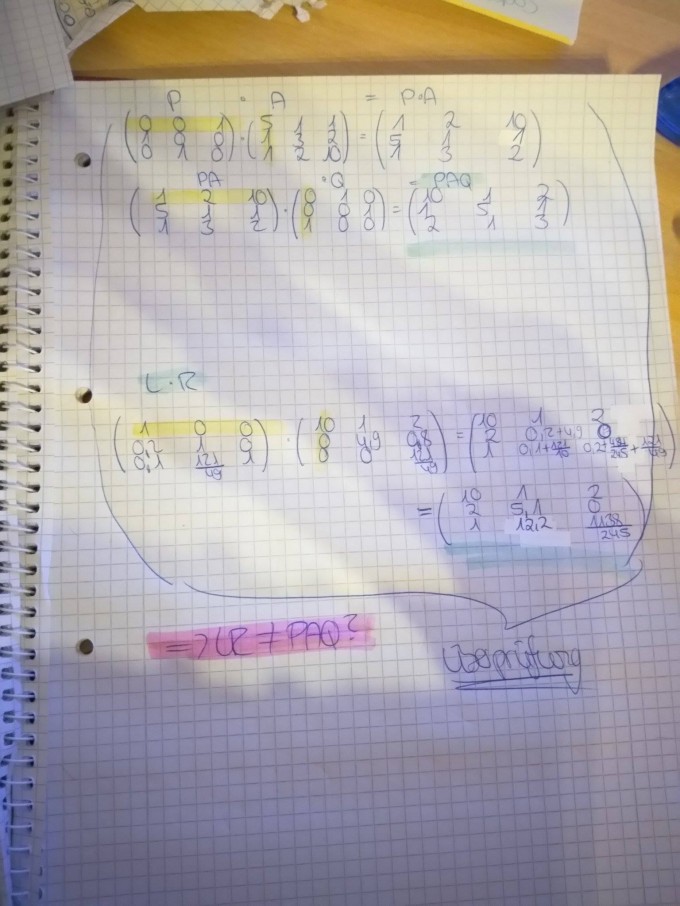
Mein Problem hierbei ist, dass ich am Ende (erstes Foto) die Gleichung PAQ = LR erhalte und wenn ich diese beiden Seiten dann ausmultipliziere, erhalte ich nicht das gleiche...

Auf dem 2. Foto sieht man, wie ich das multipliziert habe: Ich habe erst P in A multipliziert und im Anschluss PA in Q. 

Wenn ich dann die rechte Seite L * R ausmultipliziere, erhalte ich etwas anderes.

Nun bin ich unsicher, wo da mein Fehler liegt... liegt er bereits bei der Herstellung der Zerlegung oder nur bei der Multiplikation am Ende...*grübel*

Ich habe schon sehr viel im Internet gesucht, finde aber nichts was mir weiterhilft.. es gibt solche Online-Rechner, die berechnen aber nichts mit der Totalpivotisierung..

Über Antworten wäre ich wirklich sehr dankbar!!

LG, Stella

Answer 1

Hallo Stella,

Du hast

\( L_2 *P_2 * L_1 * P_1 * A * Q_1 * Q_2 = R \)

P_2 verschieben E=P2^-1 * P2 einfügen

\(  L_2 *P_2 * L_1 *P_2^{-1} P_2 *P_1 * A * Q_1 * Q_2 = R \)

zusammenfassen  \( L_0=P_2 * L_1 *P_2^{-1} \)

\(  L_2 *L_0*P_2 *P_1 * A * Q_1 * Q_2 = R \)

ausmultipliziert \(  L_0^{-1}  * L_2^{-1} = L \)

\( P* A* Q =L* R \)

Comments

erstmal vielen Dank für die Antwort.

Leider haben wir noch nicht mit Inversen usw. gerechnet, also bisher lediglich den Gauß-Algorithmus. D.h. ich sollte das sozusagen ohne machen, also die ganz normale Berechnung mit den Vertauschungen in den Permutationsmatrizen..

Deshalb verstehe ich deinen Weg gerade nicht ganz... könntest du mir vielleicht sagen, wie ich sonst noch drauf kommen kann? :(

LG, Stella

---

Nun invertieren sich L- Dreiecksmatrizen sehr einfach, es ändert sich nur das Vorzeichen unterhalb der Diagonalen. Ansonsten weiß ich nicht, wie man die Form P A Q herstellen könnte. Um L zu erhalten musst Du auch ohne Pivotsuche die Zeilenmatrizen L_1, L_2 invertieren.

Für die Permutationsmatrizen gilt \( P^{-1} = P^{T} \) - die Inverse erhält man durch Transponieren. Hier sind sie zu sich selbst Invers P^2=E.

Hier mal meine Lösung:

 

---

nochmals herzlichen Dank!! Jetzt verstehe ich das :-)

Eine Kleinigkeit noch: Ist es egal, ob ich oben bei P(1) und Q(1) von "rechts" bzw. von "links" beginne mit der mit Einsen befüllten Hauptdiagonale? Denn ich hatte begonnen in a11 und alle Einsen in a22

 und a33, also von "links" begonnen.

Und wie ich deiner Rechnung entnommen habe, müssen alle Zeilen- und Spaltenvertauschungen auch in L durchgeführt werden, oder?

Dankesehr und LG

---

Das Matrizenprodukt ist im Allgemeinen NICHT kommutativ: A B # B A

Es ist ein Unterschied ob Multiplikation von Links oder Multiplikation von Rechts. Beim Multiplizieren von L-Matrizen findet quasi ein Verschmelzen der Matrizen statt. Schau mal 

L2 * Lo an  und vergleiche mit L - hier siehst Du wie Lo in L2 reingeschoben wird, Minuse an die Elemente unter der Diagonalen und fertig ist die Inverse L.

Diese einfachen Verfahren zur Multiplikation und zum Invertieren sind mit ein Grund um mit dem Gauss-Algorithmus die L R Zerlegung zu erzeugen.