"...soll ich zeigen, dass man auch jede Folge als eine Reihe darstellen kann..."
damit ist bestimmt das gemeint, was mathef zeigte.
ABER die Überschrift als Frage -> da denkt man zunächst an was anderes:
frage mal Deinen Lehrer, wie die "Reihendarstellung" der
Primzahl-Folge aussieht ( http://www.lamprechts.de/gerd/Primzahlen.htm
Punkt 5. Prime(x)= ...
aber Dein Lehrer kennt sie bestimmt nicht)...
Aber es gibt noch viel kompliziertere Zahlenfolgen, die nur als Code- Algorithmus bekannt sind ->
( http://oeis.org/A194954 und noch kompliziertere )
daraus eine Reihe geht nur mit dem Trick, dass man Funktionen f(x) oder Glieder a[i] als bekannt annimmt und daraus eine Summe bastelt.
Oft wird auch verwechselt, dass es 2 Arten von "Reihen" gibt:
a) https://de.wikipedia.org/wiki/Reihe_(Mathematik) also "Partialsumme"
aus den Folgeglieder a[1]...a[n] die Partialsumme bilden: ∑ a[k] , k=1...n
Beispiel Primzahlen-Folge http://oeis.org/A000040
Partialsumme, also die Reihe davon: http://oeis.org/A007504
b) https://de.wikipedia.org/wiki/Reihe_(Mathematik)#Reihen_von_Funktionen
Es gibt die Primzahl-Folge: a[1]=2, a[2]=3,...
a[n]=Prime(n) -> die Primzahlfunktion: Prime(1)=2; Prime(2)=3
die Reihendarstellung dieser Funktion lautet:
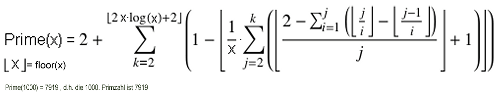
Also 2 Algorithmen für die selbe Sequenz: http://oeis.org/A000040
Um diese Verwechslung zu vermeiden, da es beides Reihen sind, sollte man besser von Partialsummen oder Reihendarstellung sprechen.