Drei veschiedene Vektoren im Raum 3 linear unabhängig beweisen

Question

Seien v₁ = (1,2,3), v₂ = (4,5,6) und v₃ = (7,8,9) Vektoren in R³. Ist B = {v_i :i = 1,2,3} linear unabhängig? Beweisen Sie Ihre Antwort.

Answer 1

mach den Ansatz

x*v1 + y*v2 + z*v3 = 0-VektorDas gibt ein Gleichungssystem für x,y,z und zeige:

Dashat nicht  nur die Lösung  x=y=z=0 .sondern etwa auch  1  -2  1 .



=>  Die Vektoren sind lin, abh,  z.B.


-1*v1 + 2*v2 = v3.

Answer 2

Jan12345, 

Du kannst diese Aufgabe lösen, indem Du die drei gegebenen Vektoren in einer Matrix zusammenfasst und die Determinante berechnest. Wenn die Determinante der besagten Matrix gleich 0 ist, dann sind die Vektoren linear abhängig. Erhältst Du einen von 0 verschiedenen Wert, dann sind die Vektoren linear unabhängig.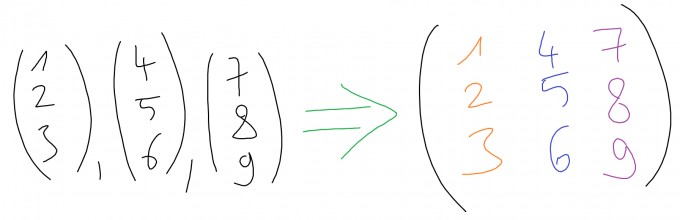 

Die Determinante dieser Matrix berechnest Du z.B. mit der Regel von Sarrus und erhältst: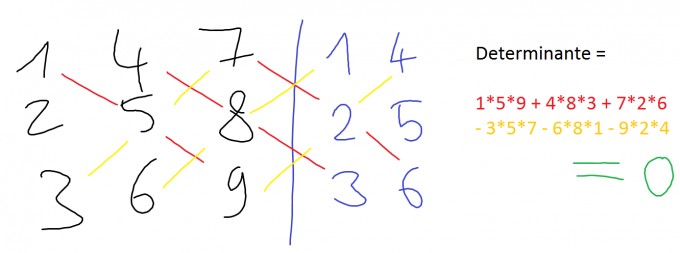 

Die Vektoren sind also linear abhängig. 

Konnte ich Dir damit weiterhelfen? Falls nein, kannst Du Dich gerne wieder melden und ich versuche einen alternativen Erklärungsansatz.

André, savest8

Comments

Soll man nicht beweisen, dass B = {v_i :i = 1,2,3} linear unabhängig ist?

---

nikeone55, 

nein. Die Aufgabe wurde als Frage formuliert, d.h. es kann linear unabhängig sein, muss es aber nicht. In diesem Fall trifft Letzeres zu.

André, savest8