wir fertigen eine Tabelle an, in der wir alle möglichen Werte, welche die X und Y annehmen können, kombinieren. Die Tabelleneinträge sind dabei die Produkte der Augenzahlen der Würfel, also $$Z1=X\cdot Y$$ wie von Dir beschrieben. In der Tabelle markieren wir, welche Ergebnisse wie oft vorkommen und erhalten: 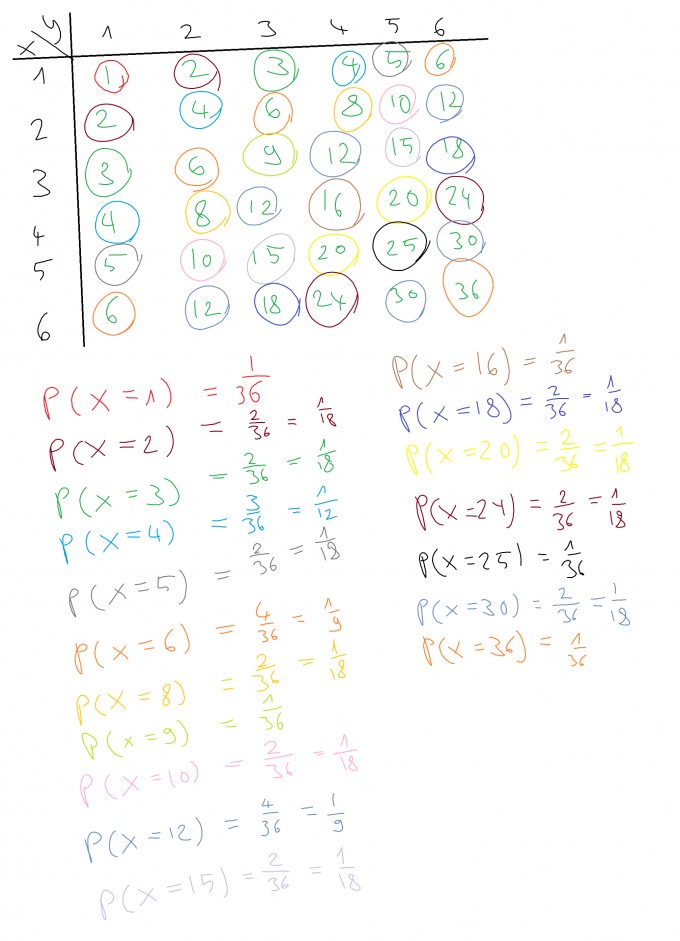
Den Erwartungswert für die Zufallsvariable Z1 erhältst Du nun, indem Du die Werte von Z1 mit ihren entsprechenden Wahrscheinlichkeiten multiplizierst: $$E(Z1)=1\cdot \dfrac{1}{36}+2\cdot \dfrac{1}{18}+3\cdot \dfrac{1}{36}+...+36\cdot \dfrac{1}{36}=\dfrac{49}{4}=12.25=3.5^2$$ Dieses ist übrigens nicht verwunderlich: Der Erwartungswert beim Werfen eines Würfels mit den Augenzahlen 1, 2, 3, 4, 5 und 6 liegt nämlich bei 3.5. Der Erwartungswert beim Werfen zweier Würfel folglich bei $$3.5\cdot 3.5=3.5^2=12.25$$ Konnte ich Dir damit weiterhelfen? Stelle gerne Rückfragen, wenn etwas unklar geblieben sein sollte.
André, savest8
PS: Die Tabelle ist übrigens symmetrisch. Dadurch könntest Du Dir einiges an Schreibaufwand ersparen.
