Dmax, Wmax, Monotonie

Question

Mahlzeit zusammen! Wäre sehr froh wenn mir jemand bei dieser Aufgabe helfen könnte, habe gar keine Ahnung wie ich an die Sache herangehen soll.

Vorgelegt sei die Funktion

f(x) = ln(−(x−2)(x + 3)).

Bestimmen Sie den maximalen Definitionsbereich D und den Wertebereich W von f. Untersuchen Sie f auf Monotonie und geben Sie die maximalen Teilintervalle von D an, auf denen f monoton ist.

Answer 1

f(x) = LN(- (x - 2)·(x + 3))

Wenn du mal nur das Argument vom LN untersuchst

y = - (x - 2)·(x + 3)

Hier hat man eine nach unten geöffnete Parabel mit den Nullstellen bei -3 und +2. Zwischen den Nullstellen hat man positive Funktionswerte. Daher (weil das Argument im LN nur positiv sein darf) ist die Definitionsmenge deiner Funktion.

D = ]-3 ; 2[

Für die Wertemenge bestimmt man das Maximum des Argumentes, welches sich zwischen den Nullstellen bei -0.5 befindet.

y = - (-0.5 - 2)·(-0.5 + 3) = 6.25

Das Der Wertebereich der Funktion ist also

W = ]-∞ ; LN(6.25)]

Das Argument ist im Intervall von ]-3 ; -0.5] streng monoton Wachsend und im Intervall [-0.5 ; 2[ streng monoton fallend. Weil der LN(x) streng monoton wachsend ist gilt die Monotie für das Argument genauso für die Funktion.

Answer 2

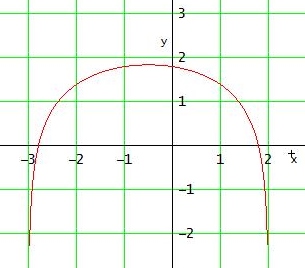
f(x) = ln(- (x - 2)·(x + 3))          ist nur für positive Werte im ln definiert

Der Term   - (x - 2)·(x + 3)  steht für eine nach unten geöffnete Parabel, deren Funktionswerte genau zwischen den Nullstellen x₁ = -3 und x₂ = 2 positiv sind                       →  D = ] -3 ; 2 [

f '(x) = (2·x + 1) / ((x - 2)·(x + 3))

f '(x) = 0  ⇔_D   2x+1 = 0   ⇔  x = -1/2  mit Vorzeichenwechsel von + → -

→   Maximum in H( -1/2 | 2 * ln(5/2) )  ≈  H( -1/2 | 1,83)

Die Monotonie wird durch das Vorzeichen von f '(x) bestimmt:

f '(x)  ≥  0  für x ∈ ] - ∞ ; -1/2 ]   →  f  streng monoton wachsend 

f '(x)  ≤  0  für x ∈ [ - 1/2 ; ∞ [    →  f  streng monoton fallend

lim_x→-3+ f(x) = lim_x→-3+ f(x)  = - ∞    →     Wertemenge    W_f = ] -∞ ; 2 * ln(5/2) [  

( ln(Term) → ∞ für Term → 0)

Gruß Wolfgang