Question

Bestimmen Sie die Werte für b so, dass ihr Schaubild K eine behebbare Lücke hat.

Vielen Dank

Answer 1

Guten Morgen anhtran226,

eine hebbare Stelle liegt hier vor, wenn der Nennerterm für einen bestimmten x-Wert 0 ergibt und das Problem der Division durch 0 mittels Polynomdivision gelöst werden kann (der Bruchterm wird dann ohne Definitionsproblem dargestellt). Wir führen zuerst eine Polynomdivision des Zählers mit \(x=1\) als Nullstelle durch und erhalten:

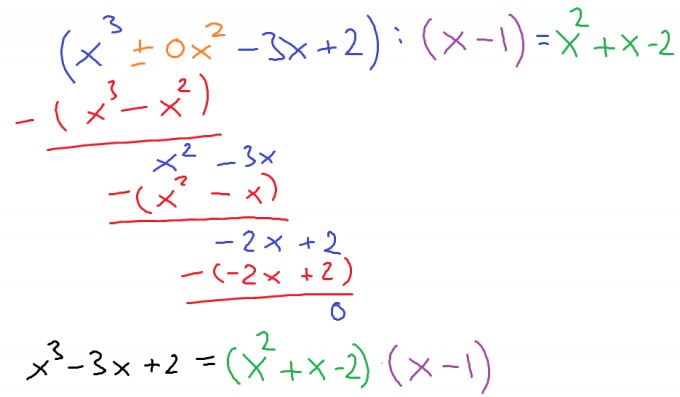
Weiterhin ist $$x^2-bx=x\cdot(x-b)$$ Für \(b=1\) folgt:

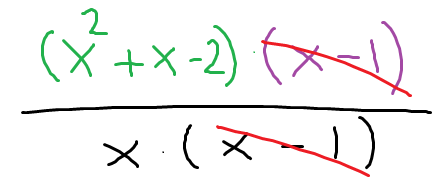
und es gibt eine hebbare Stelle bei \(x=1\).

André, savest8

Comments

Auch  hier würde ich gerne wissen, weshalb. Leider hast Du meine Rückfrage auf die andere Antwort ebenfalls noch nicht beantwortet. Du könntest zumindest eine Alternativlösung anbieten, damit der Fragesteller auch etwas davon hat.

---

Das kann so sein oder

---

Hallo anhtran226,

richtig. Wenn Du ein weiteres mal die Polynomdivision an der Nullstelle \(x=1\) durchführst, erhältst Du \((x - 1)^2 (x + 2)\). Wenn Du nun für \(b=-2\) wählst, dann hast Du eine weitere Stelle gefunden, denn

Grüße

---

Antwort ist b = 1 oder b= -2. Ja?

Vielen Dank für Ihre Hilfe.

---

Ja, das ist richtig.

---

f(x)=(x²-5x+6)/(x²-6x+a)

noch eine Frage wie kann man a finden, um das Schaubild K eine behebbare Lücke zu haben

Answer 2

(x^3 - 3·x + 2) / (x^2 - b·x) = ((x + 2)·(x - 1)^2) / (x·(x - b)) 

also b = -2 oder b = 1

Comments

Guten Morgen Der_Mathecoach,

das Zählerpolynom ist \(x^3-3x+2\) und nicht \(x^2-3x+2\).

---

Oh sorry. Hab das verbessert.

---

Super. Eine Frage hätte ich noch: Wie konntest Du jetzt noch Deine Antwort verbessern? Erhält man mit einem höheren Rang eine längere Bearbeitungszeit?
Beste Grüße

---

"Mitglieder" haben meines Wissens 15 Minuten Bearbeitungszeit. Kann sein, dass das mittlerweile sogar etwas erhöht wurde. Moderatoren haben 7 Tage. Redakteure unbegrenzt :).

Grüße

---

Vielen Dank Unknown! Dann werde ich mal weiter auf den Moderatoren-Status hinarbeiten;-)

---

Viel Spaß dabei :D.

Solltest Du bis dahin einen Fehler haben, den Du im Originalpost ausgebessert haben willst, dann schreibe einen Kommentar mit dem Änderungswunsch und melde einen beliebigen Post (bspw die Frage selbst) und ein Redakteur kümmert sich drum :).