Lösungsmenge mithilfe eines Tupels k = (100, 120, 250) anhand der Gleichung x=Ax+k bestimmen

Question

Aufgabe d) 

Aufgabe d)

Zu aller erst muss ich fragen was ein Tupel ist, wir haben den Begriff im Unterricht nicht behandelt.

Damit ich k addieren kann muss ich A•x ausrechnen. Allerdings aber ich lediglich die Matrix A, sowie die Form der Lösungsmenge. Ich verstehe nicht ganz wie ich die Lösungsmenge errechne wenn sie in der dazu benötigten Formel enthalten ist.

Answer 1

Guten Tag Orangedrop,

ich zeige Dir das Vorgehen exemplarisch an dem ersten Aufgabenteil.

Ein Tupel ist zunächst einmal eine geordnete Zusammenfassung von Objekten. \(\{100,120,250\}\) ist eine Menge und \((100,120,250)\) ist ein Tupel, bei dem die Position der einzelnen Einträge wichtig ist. Hier ist lediglich der Vektor k damit gemeint.

Zuerst kannst Du die Gleichung wie folgt umformen:

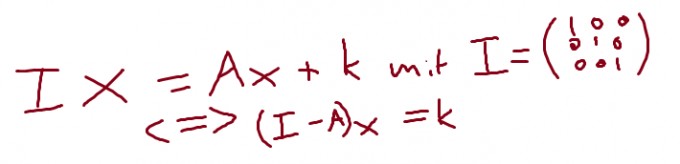
Nun subtrahierst Du die beiden Matrizen voneinander.

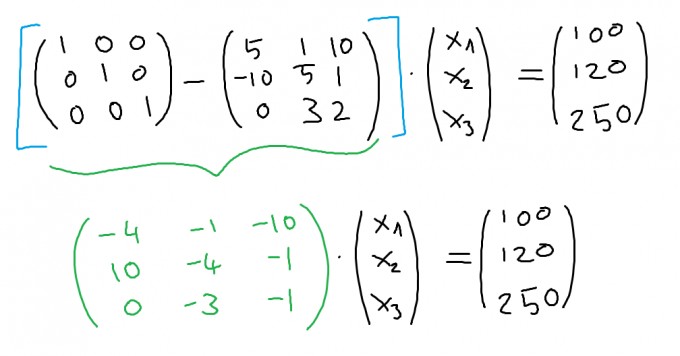
Zur Lösung dieses Gleichungssystems bildest Du die Inverse der grünen Matrix und wendest den Ansatz zur Lösung von linearen Gleichungssystemen an:

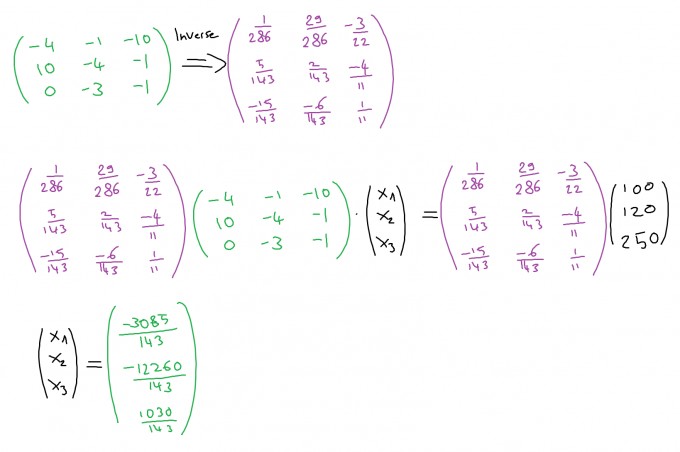
Dass dieses Ergebnis stimmt, kannst Du hier prüfen.

Hilft Dir das weiter?

André, savest8

Comments

Wozu errechnet man die Inverse und Wieso muss die Inverse sowohl mit der Matrix als auch mit dem Vektor multipliziert werden?

Nachdem die Gleichung umgestellt wird und die Matrix inkl. Inverse errechnet wird, hätte man doch einfach A * k rechnen können? Wozu dient die Inverse wenn die Formel zur Errechnung der Lösungsmenge     x = A^{-1} * k   und somit    A * x = k     lautet?

---

Hallo Orangedrop,

weißt Du, woher diese Lösungsformel kommt? $$\underbrace{A^{-1}\cdot A}_{=I}\cdot x=A^{-1}\cdot k\Longleftrightarrow x=A^{-1}\cdot k$$ Die Inverse steht aus Vollständigkeitsgründen vor \(A\cdot x\).

Wie hast Du es denn gelöst?

---

Ach natürlich. Ich hab dies gar nicht in Betracht gezogen. Aber es ist nötig oder?

Tausend dank!

---

Hallo Orangedrop,

ja, die Inverse muss tatsächlich berechnet werden, um das Gleichungssystem zu lösen. Leider sind die Ergebniswerte etwas krumm;-)

Gerne wieder! Es freut mich, dass Du die Aufgabe nun lösen kannst.

André, savest8

Answer 2

Tipp:  \(x=A\cdot x+k\Leftrightarrow(E-A)\cdot x=k\).

Comments

Wie kommst du darauf?

---

Es ist \(E\cdot x=x\).