Umkehrfunktion bestimmen von f(x)= 1/2 x2 - 2

Question

habe ein Problem und zwar würde ich die Umkehrfunktion bestimmen wollen, nur leider komme ich auf ein anderes Ergebnis.

Ich hoffe ihr könnt mir den Rechenweg angeben, damit ich sehe wo mein Fehler steckt.

Die Gleichung:

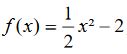
Umkehrfunktion bestimmen von f(x)= 1/2 x² - 2 

Answer 1

Ist $y=\frac{1}{2}x^2-2$ dann folgt $x=g(y)$ aus

$$y=\frac{1}{2}x^2-2$$

$$y+2=\frac{1}{2}x^2$$

$$2(y+2)=x^2$$

$$x=\sqrt{2(y+2)}$$

Anbei die Graphen

Plotlux öffnen

f₁(x) = x²/2-2f₂(x) = √(2x+4)f₃(x) = -√(2x+4)f₄(x) = x

Die blaue Parabel ist an der Winkelhalbierenden (f(x)=x) gespiegelt. Streng genommen existiert die Umkehrfunktion nur für Werte von  $x \ge0$ und $y \ge -2$ sind (roter Ast im Graphen).

Comments

Danke für die Antwort.

Die 1/2 kommen einfach mit dem Kehrwert rüber ?

---

Ja - einfach mit 2 mal nehmen, bzw. durch 1/2 teilen (ist das gleiche)

Answer 2

y=x²/2-2;  x und y vertauschen x=y²/2-2 und nach y auflösen x+2=y²/2 oder 2x+4=y². Das ergibt zwei mögliche Umkehrfunktionen y=√(2x+4) und y=-√(2x+4). Wahlweise ist f^-1(x)=√(2x+4) oder f^-1(x)=-√(2x+4.