Vektoren, stimmen die Aussagen?

Question

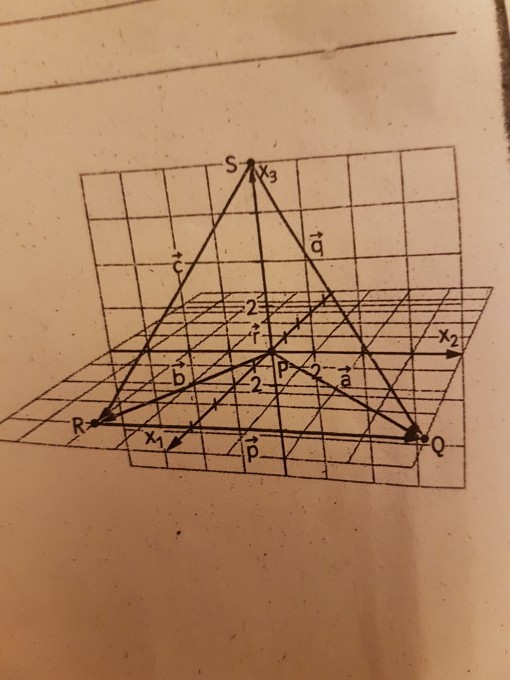
leider weiß ich nicht wie man die Pfeile macht, aber es sind alles Vektoren.

a=PQ, b= PR, c= SR, p=RQ, q=SQ und r=PS

Aussagen:

1. r+q=a

2. p=-b+r+q

3.a-p-c=r

4. q-p+c=0

Aussage 1 und 2 müssten falsch sein. Aussage 2 und 4 bin ich mir nicht sicher. Falls ihr die Antwort kennt, könntet ihr mir erklären, warum Aussage 2 und 4 entweder wahr oder falsch sind? Bei vier, soll das eine Null sein? Bedeutet das also dass alle werte 0 sind bei diesem Vektor?

Answer 1

a=PQ, b= PR, c= SR, p=RQ, q=SQ und r=PS

Aussagen:

1. r+q=a --> richtig

PS + SQ = PQ erkennst du die richtigkeit an dieser schreibweise ?

Wenn du von P nach S gehst und dann von S nach Q kann man auch gleich von P nach Q gehen.

Schreibe dir das auch für die anderen Beispiele so auf.

2. p=-b+r+q --> richtig

3. a-p-c=r --> richtig

4. q-p+c=0 --> falsch

Comments

Ich verstehe das noch nicht ganz. Ich dachte, dass man eine Art Dreieck hat und die "kleinen" Vektoren addiert der "große" Vektor ergibt, also die große Seite des Dreiecks.Und groß minus klein die andere kleine Seite. Das wie du das erklärst verstehe ich zwar, aber nicht warum das funktioniert. Bei Youtube gibt es nicht wirklich hilfreiche Videos. Falls du eine Seite hättest speziell zu dieser Aufgabe, wäre ich dir sehr dankbar, wenn du mir sie schicken könntest.

---

Es stimmt schon das Man oft Dreiecke betrachten kann.

Generell kannst du dir meine Erklärung merken.

AB + BC = AC

Ein Vektor geht von A nach B. Einer geht von B nach C. Dann kann ich die Summe als einen Vektor schreiben, der von A nach C geht.

Ebenso kannst du diese Gleichung umformen.

AB = AC - BC

BC = AC - AB

Es ist ja nicht nur wichtig an welchen Seiten die Vektoren sind sondern auch in welche Richtung sie weisen.