Zu Deiner ersten Frage: die größte Abmessung in einem regelmäßigen Fünfeck ist eine der Diagonale. Ist die Seitenlänge \(a\) so misst die Diagonale \(d=a\frac{1}{2}(\sqrt{5}+1)\). Hat das Quadrat die Seitenlänge \(d\) so wurde das Fünfeck hinein passen.
Umgekehrt gilt, wenn \(d=50\text{m}\) gegeben ist, berechnet sich \(a\) aus
$$a=d\frac{1}{2}(\sqrt{5}-1)=50\text{m} \cdot \frac{1}{2}(\sqrt{5}-1) \approx 30,90 \text{m}$$
Die Fläche \(F\) des Fünfecks ist \(a^2\frac{1}{4}\sqrt{25 + 10\sqrt{5}}\) mit bekanntem \(d\) wird daraus
$$F=d^2 \cdot \frac{1}{16}(\sqrt{5}-1)^2 \cdot \sqrt{25 + 10\sqrt{5}} \approx 1642,91\text{m}^2$$
anbei eine Skizze zur Kontrolle:
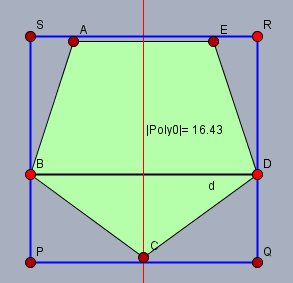
Bem.: man könnte das Fünfeck natürlich auch noch etwas drehen! Ich schreibe später noch einen Kommentar dazu!
Um den Rest Deines Mathematikbeispiels zu lösen, benötigt man noch mehr Informationen darüber, wo sich die Punkte A', B' und C' befinden sollen. Liegen B' und C' auf der Symmetrieachse des Fünfecks? Soll C'A' parallel zu AE liegen? Falls beides bejaht wird und falls C' dann noch auf dem Umkreis des Fünfecks liegen soll, so ist die Aufgabe IMHO nicht lösbar.
Schaue Dir folgendes Bild an. Die schwarze Parallele hat einen Abstand von \(r\) zu AD. Auf ihr kann man den Inkreismittelpunkt \(I\) verschieben, aber es gelingt nie den Punkt \(A'\) auf die blaue Gerade durch \(C\prime\) zu schieben.
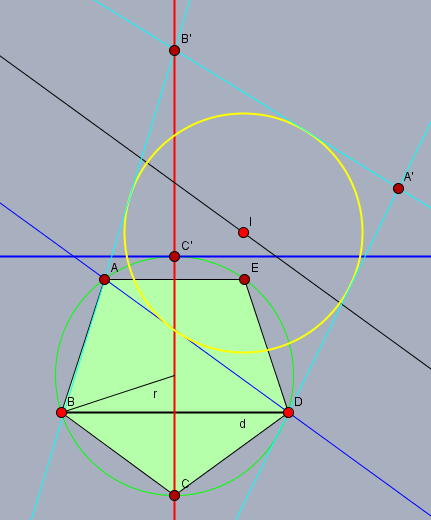
Wie sind die Informationen zu den Position der Punkte A', B' und C' ?
BTW: ist die Fläche AEDA' oder die Fläche von ADA'B' gesucht?
Gruß Werner