Lösen lineares Gleichungssystem

Question

Hallo
kann mir vielleicht jemand erklären wie ich dieses lineare Gleichungssystem Schritt für Schriit nach c2, c1 und c0 auflösen kann?

y_a = c₂ * a² + c₁ * a + c₀

y_b = c₂ * b² + c₁ * b + c₀
y_m = c₂ * ( (a+b) / 2 ) ² + c₁ * ( (a+b) / 2 ) + c₀

Answer 1

Lineare Gleichungssysteme löst man mit dem Gaußschen Eliminationsverfahren.  Siehe https://de.wikipedia.org/wiki/Gau%C3%9Fsches_Eliminationsverfahren.  Dort ist ein ausführliches Beispiel, 3 Gleichungen mit 3 Unbekannten.  Kommst du mit dem klar?

Comments

Ja den Gauß Algorithmus kenne ich......kann ich dieses LGS also auch damit lösen??

---

Ja, genau.  Nur dass in Wikipedia Zahlen stehen und in deiner Aufgabe Variablen.  Inzwischen hat es Georg ja durchgerechnet, siehe unten.

Answer 2

y_a = c₂ * a² + c₁ * a + c₀
y_b = c₂ * b² + c₁ * b + c₀  | abziehen
---------------------------------
ya - yb = c2 * ( a^2 - b^2 ) + c1 * ( a - b )

y_b = c₂ * b² + c₁ * b + c₀ 
y_m = c₂ * ( (a+b) / 2 ) ² + c₁ * ( (a+b) / 2 ) + c₀ | abziehen
------------------------------------------------------------
yb - ym = c2 * ( b^2 - ((a+b)/2 )^2 - c1 * ( b -(a+b)/2 )

ya - yb = c2 * ( a^2 - b^2 ) + c1 * ( a - b )
yb - ym = c2 * ( b^2 - ((a+b)/2 )^2) + c1 * ( b -(a+b)/2 )

ersetzen
d1 = ( a^2 - b^2 )
d2 = ( b^2 - ((a+b)/2 )^2)

ya - yb = c2 * d1 + c1 * ( a - b ) | * d2
yb - ym = c2 * d2 + c1 * ( b -(a+b)/2 ) |  d1

( ya - yb ) * d2 = c2 * d1 * d2 + c1 * ( a - b ) * d2
( yb - ym ) * d1= c2 * d2 * d1+ c1 * ( b -(a+b)/2 ) * d1
--------------------------------------------------------------------
( ya - yb ) * d2 - ( yb - ym ) * d1
=  c1 * ( a - b ) * d2 -  c1 * ( b -(a+b)/2 ) * d1

c1 =  [ ( ya - yb ) * d2 - ( yb - ym ) * d1 ] /
[ ( a - b ) * d2 -  ( b -(a+b)/2 ) * d1 ]

Jetzt noch d1 und d2 zurückersetzen.

Mein Matheprogramm bekommt heraus : c1 =

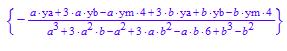
Was ist die Aufgabe ? Eine Strafarbeit ?

mfg Georg

Comments

" Strafarbeit? "

Kann sein, dass ich hier https://www.mathelounge.de/427265/herleitung-der-simpsonregel eine Herleitung verlinkt habe, die diese Umformung dem Leser überlässt. 

---

Die Lösung kann nicht stimmen. Wähle z.B. a = b.

---

@nn: a=b ist bei der Simpson-methode nicht von Interesse. Sollte aber hier zu Beginn so in der Aufgabenstellung angegeben worden sein. 

---

Das LGS hat für a = b keine (eindeutige) Lösung. Nach obiger Lösung ist aber c₁ eindeutig, falls zusätzlich a ≠ 0 und a ≠ 1 ist. Daher kann diese Lösung nicht stimmen.

---

@Lu Nein dieses LGS stammt nicht von der Seite die du mir verlinkt hast, aber es geht tatsächlich um die Herleitung von Kepler's Fassregel zur Berechnung von Integralen. Nur fehlte mir der Ansatz zur Lösung.....ich bin im Moment dabei es mit einsetzen zu versuchen, also nach zum Beispiel c1 umstellen und dies dann ersetzen usw.

---

Im Nachhinein wäre es wohl besser
(a+b) / 2 von Anfang an durch z.B. d zu ersetzen.

--------
ich habe gerade die 3 Ausgangsformeln nochmals
mit meinem Matheprogramm berechnet.
Es kommt dieser Lindwurm heraus.

Bist du dir sicher das Kepler so gerechnet hat ?

---

Ob Kepler es persönlich so berechnet hat wäre eine interessante Frage :D

Ich habe diese Herleitung hier gefunden: http://www.herder-oberschule.de/madincea/aufg1213/kepler1.pdf

Wobei ich sagen muss, dass mir diese Herleitung allgemein schwer fällt nachzuvollziehen aber dafür kommt genau das raus was ich suche ! :D