Reihe auf Konvergenz untersuchen: n!/n^n

Question

habe die folgende Frage... ich habe dies mit dem Quotientenkriterium gemacht und dann gesehen, dass es die e-funktion form ist und dann mit Tricks herausgefunden dann die Reihe gegen 1/e konvergiert und damit <1 und somit konvergent ist:

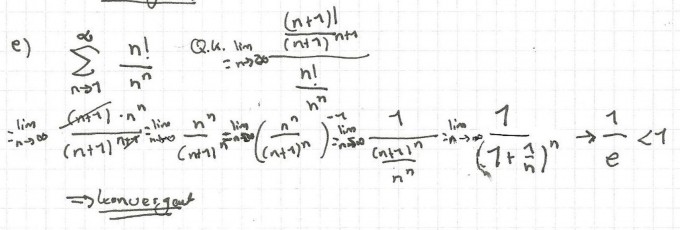
Aber könnte ich ab $${ (\frac { n }{ n+1 } ) }^{ n } $$ auch das wurzelkriterium anwenden wie folgt:

$$\sqrt [ n ]{ { (\frac { n }{ n+1 } ) }^{ n } } =_{ n\rightarrow \infty  }^{ lim }{ \frac { n }{ n+1 }  }<1\quad ->\quad konvergent$$

ist das so auch möglich?

MFG

Comments

Wie kommst Du denn auf \(\lim_{n\to\infty}\frac{n}{n+1}<1\) ?

Ansonsten: Ist Dir ueberhaupt der Unterschied zwischen Folgen und Reihen klar? Das Wurzelkriterium ist für Reihen, nicht für Folgen.

---

d.h. also kann ich da nicht einfach in der mitte auf WZ umsteigen sonndern muss es mit dem QK zu ende führen? .. naja n/n+1 ist immer kleiner als 1... dann wäre doch das Wurzelkriterium damit erfüllt denn es besagt ja |x|< 1 -> konvergent:D

---

Das Wurzelkriterium ist für Reihen, nicht für Folgen. Und für \(\sqrt[n]{|a_n|}<1\) lefert es keine Aussage.

Answer 1

Ja, und es geht sogar noch genauer, also nicht nur dass konvergiert, sondern den Wert selbst:

Bekannt ist die

https://de.wikipedia.org/wiki/Stirlingformel

n!=n^n*sqrt(2Pi*n)*(1+1/(12n)+1/(288n²)+...)/e^n

also kürzt sich n^n heraus und über bleibt:

sum sqrt(2Pi*n)*(1+1/(12n)+1/(288n²))/e^n, n=1...∞

=1,88...

exakter:

https://www.wolframalpha.com/input/?i=sum+n!%2Fn%5En,n%3D1...inf

Comments

Hallo

ist lange her aber hab dir trotzdem mal den Plus gegeben, da ich alles wiederholen muss für die Klausur demnächst.. danke sehr

ich glaube oben hat Fakename nicht genau verstanden, dass es hier um die Konvergenz von einer Reihe geht und somit das Wurzel Kriterium in Ordnung ist?

---

Das Wurzelkriterium führt hier zu nichts, da

$$ \lim_{n\to\infty}\frac{n}{n+1}=1 $$

Somit ist mit dem Wurzelkriterium keine Aussage möglich.

Verwende stattdessen das Quotientenkriterium wie in der Musterlösung.

---

$$\lim_{n\to\infty}\frac{n}{n+1}=1$$ ist das nicht 0?

$$\lim_{n\to\infty}\frac{n/n}{n/n+1/n}$$

$$\lim_{n\to\infty}\frac{1}{1}=1$$

bzw. wenn das so geht dann hast du natürlich recht, aber ich muss nicht den Grenzwert einer Folge bestimmen, sondern untersuchen, ob die Reihe konvergiert:

Aber ich dachte Beim WK eher an

$$\sqrt [ n ]{ |{ (\frac { n }{ n+1 } ) }^{ n }| } =\frac { n }{ n+1 } <1$$

das ist ja offensichtlich < als 1 die Folge oben (n/(n+1) konvergiert aber gegen 1 ist ja klar aber was sagt das jetzt über die Reihe aus?

wo steckt mein Denkfehler?

---

egal hat sich geklärt... ich muss das Quotientenkriterium anwenden und komme wie oben auf 1/e das < als 1 ist und somit ist die Folge konvergent...

mich hat hyperG nur etwas verwirrt deswegen. :D