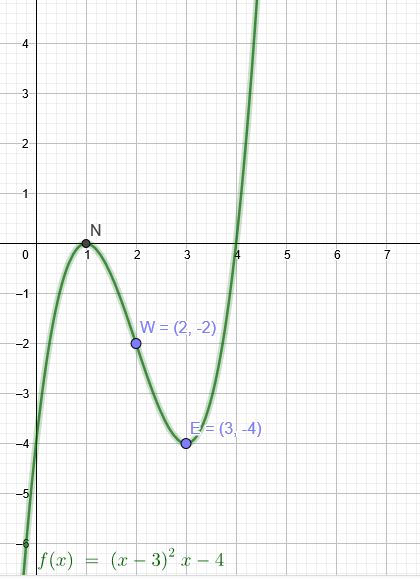
"Ermittle die Koeffizienten einer Polynomfunktion 3. Grades , deren Graph, in E (3| -4) einen Extremwert hat und an der Stelle x = 2 einen Wendepunkt hat . Außerdem schneidet die Funktion die x- Achse an der Stelle x= 1"
\(E (3| -4)\) einen Extremwert →\(E´ (3| 0)\) doppelte Nullstelle
x=1 ist Nullstelle: \(N(1|0)\) \(N´(1|4)\)
\(f(x)=a*(x-3)^2*(x-N)\)
\(N´(1|4)\):
\(f(1)=a*(1-3)^2*(1-N)=4a*(1-N)=4\) \(a=\frac{1}{1-N}\)
\(f(x)=\frac{1}{1-N}*[(x-3)^2*(x-N)]\)
Wendepunkt bei \(x = 2\) :
\(f´(x)=\frac{1}{1-N}*[(2x-6)*(x-N)+(x-3)^2*1]\)
\(f´´(x)=\frac{1}{1-N}*[2*(x-N)+(2x-6)+2*(x-3)]\)
\(f´´(2)=\frac{1}{1-N}*[2*(2-N)+(2*2-6)+2*(2-3)]=0\)
\(N=0\) \(a=1\)
\(f(x)=(x-3)^2*x\)
\(p(x)=(x-3)^2*x-4\)
Ausmultiplizieren,um die Koeffizienten zu bekommen.
Außerdem schneidet die Funktion die x- Achse an der Stelle x= 1
Besser: Außerdem berührt die Funktion die x- Achse an der Stelle x= 1.