a) Zeichnen sie zunächst den Graphen!
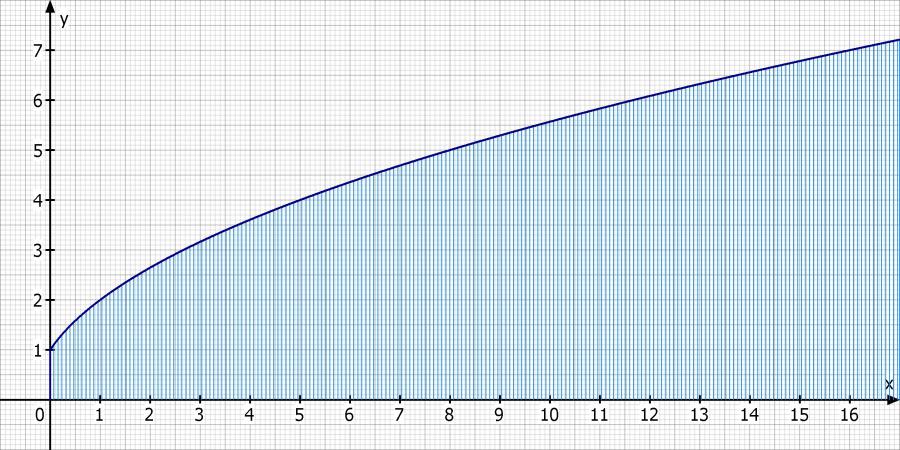
b) Berechnen sie das Volumen dieser Schale.
v(x) = pi * (3x + 1)
V(x) = 3/2·pi·x^2 + pi·x
V(5) = 85/2·pi = 133.5 cm^3
c) In die Schale wird 0,1 Liter Wasser eingefüllt. Wie hoch steht das Wasser im Gefäß?
V(x) = 100
3/2·pi·x^2 + pi·x = 100
x = (√(pi + 600) - √pi)/(3·√pi) = 4.285 cm
d) Welche Höhe muss die Schale mindestens haben, damit sie ¼ Liter Wasser fasst?
V(x) = 250
3/2·pi·x^2 + pi·x = 250
x = (√(pi + 1500) - √pi)/(3·√pi) = 6.958 cm
e) Berechnen sie das Volumen, das entsteht, wenn der Graph der Funktion f um die y-Achse rotiert.
y = √(3·x + 1)
3·x + 1 = y^2
3·x = y^2 - 1
x = 1/3·y^2 - 1/3
y = 1/3·x^2 - 1/3
Hier ist unklar wie mit dem Teil unter der x-Achse verfahren werden soll.