Hi Finja,
beim Differenzenquotienten wird das Steigungsdreieck zwischen 2 Punkten des Graphen betrachtet und
[f(x2) - f(x1)] / (x2 -x1)
berechnet.
Man schreibt dann für x2 : x0 + h
und lässt dieses h ganz klein werden, so dass man ein winziges Steigungsdreieck erhält und damit die Ableitung bzw. den Anstieg an dieser Stelle.
Machen wir das mal:
a)
f(x) = x2 an der Stelle x0 = -1
Differenzenquotient:
[f(x0 + h) - f(x0)] / [(x0 + h) - x0]
x0 = -1 einsetzen:
[(-1 + h)2 - (-1)2] / [(-2 + h) - (-2)]
(1 - 2h + h2 - 1) / (-2 + h + 2)
(h2 - 2h) / h
Im Zähler h ausklammern ergibt
h (h - 2) / h
Durch h gekürzt
h - 2
Wenn h beliebig klein wird, strebt h - 2 natürlich gegen -2,
und das ist genau der Anstieg der Funktion im Punkt x0 = -2
f(x) = x2
f'(x) = 2x
f'(-1) = 2 * (-1) = -2
Bei den anderen Aufgaben geht man genauso vor.
Graphen zeichnen ist ja ganz einfach:
Du erstellst Dir eine kleine Wertetabelle, gehst den jeweiligen x-Wert nach rechts oder links und den jeweiligen y-Wert nach oben oder unten.
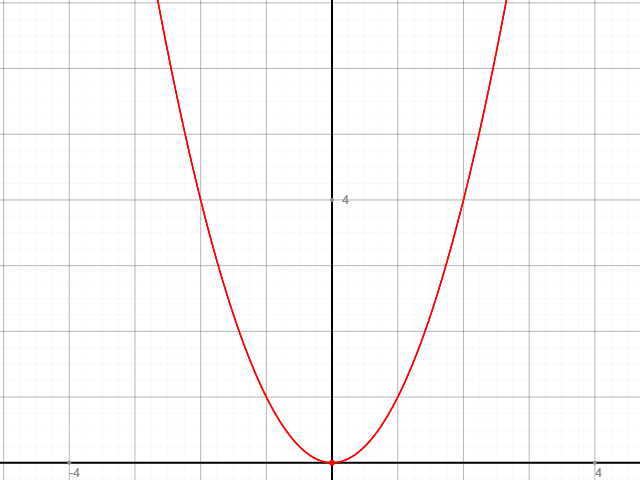
Beispiel f(x) = x2
x f(x)
-2 4 ein Punkt an der Stelle (-2|4)
-1 1 ein Punkt an der Stelle (-1|1)
0 0 ein Punkt an der Stelle (0|0)
1 1 ein Punkt an der Stelle (1|1)
2 4 ein Punkt an der Stelle (2|4)
Eine Tangente kannst Du folgendermaßen einzeichnen:
Wir hatten gesehen, dass die Funktion f(x) = x2 an der Stelle x0 = -1 die Steigung -2 hat. Du gehst also an den Punkt (-1|1)
- denn f(-1) = 1 -
und zeichnest die Tangente, die ja auch die Steigung -2 hat so ein:
Eine Stelle nach rechts (x0 + 1) und 2 Stellen nach unten.
Dann bist Du an der Stelle (0|-2). Diese Gerade kannst Du jetzt beliebig in beide Richtungen verlängern und hast damit die Tangente am Punkt (-1|1).
Besten Gruß