Unter der Annahme, dass der rechte Winkel des Dreiecks (bei B) Teil des Rechtecks sein soll (eine andere Möglichkeit hat gast hj2166 skizziert)
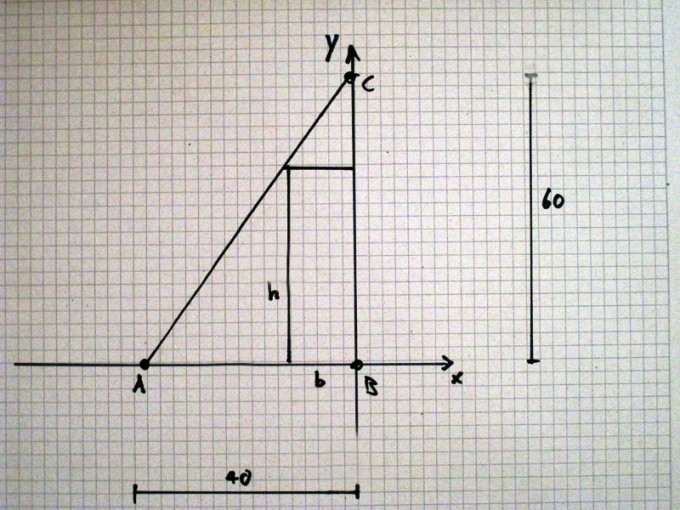
gibt es diverse Ansätze zur Lösung. Zu maximieren ist jeweils die Fläche = b h des Rechtecks. Die bei jedem Lösungsansatz gefundene Gleichung mit b und h muss entweder nach b oder nach h aufgelöst werden, und dann eingesetzt werden in die zu maximierende Funktion b h. Das Maximum ist dort, wo die erste Ableitung der Flächenfunktion null ist.
A) Strahlensatz
Wenn Punkt A der Scheitel der beiden Strahlen ist, dann gilt der (m.E. zweite) Strahlensatz "Es verhalten sich die Abschnitte auf den Parallelen wie die ihnen entsprechenden, vom Scheitel aus gemessenen Strecken auf jeweils derselben Geraden":
60 / h = 40 / (40-b)
B) Steigung von AC
h = 60 - 3/2 b
C) Satz des Pythagoras
√((40 - b)2 + h2) + √(b2 + (60-h)2) = √(402 + 602)
woraus folgt h = -3/2 (b - 40)
D) Trigonometrie
tan α = 60 / 40 = h / (40 - b)
E) Integralrechnung
Man integriert über die ganze Breite hinweg die Höhe h und erhält so den Flächeninhalt:
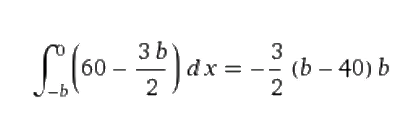
wobei die rechte Seite der Gleichung wiederum zu maximieren ist.