Gradient von f und x im Skalarprodukt ergeben f(x)?

Question

folgende Aufgabe auf deren Lösung ich einfach nicht komme:

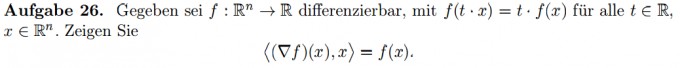
Das Skalarprodukt ist ja einfach die Summe der einzelnen Zeilen im Vektor x_i multipliziert mit den Spalten im Vektor y_i. (Bezogen auf (x,y) im Skalarprodukt.

Für die obige Aufgabe bedeutet das also, dass ich die partielle Ableitung nach x_i mit den Vektorzeilen jeweils multiplizieren und summieren muss? Wie zeige ich, dass das f(x) ergibt? Kann mir vielleicht jemand ein einfaches Beispiel geben, damit ich verstehe, was gemeint ist?

Und bedeutet f(t•x) = t • f(x) schon, dass die Abbildung linear ist? Dafür fehlt doch eigentlich noch die Additivität?

Comments

Und was genau ist mit überhaupt mit dem x in dem Skalarprodukt gemeint? Sind das alle variablen in f(x) oder wie?
Also bei f(x) = 2x+y wäre x = (x,y)^t ? Denkfehler?

---

Zeigen, dass [grad f(x), x ] = f(x)

Sei f : R^n → R differenzierbar, mit f(t · x) = t · f(x) für alle t ∈ R, x ∈ R^n.

Wie zeige ich, dass dann [grad f(x), x ] = f(x) gilt?

---

Tipp: Google homogene Funktion, Satz von Euler

---

@ullim

Infofrage:

Mir ist klar, das hier nichts Anderes gemeint sein kann, aber

ist   [grad f(x), x ]  als Schreibweise für das Skalarprodukt  < grad f(x), x >  inzwischen "allgemein akzeptiert" ?  

---

Nein, meines Wissens nicht. Schlampige Schreibweise des Fragestellers.

Answer 1

Hi,
sei \( g(t) = f(tx) \) dann gilt
$$ \frac{d}{dt} g(t) = \frac{d}{dt} f(tx) = \nabla f(tx) \cdot x $$ und andererseits
$$ \frac{d}{dt} g(t) = \frac{d}{dt} f(tx) = \frac{d}{dt} t f(x) = f(x)  $$ also insgesamt für \( t = 1 \)
$$ \nabla f(x) \cdot x = f(x)  $$

Comments

Zum ersten Teil:
Warum genau das d und nicht das geschwungene d für die partielle Ableitung?
Und warum ist d/dt f(tx) = grad(f(tx)) • x ? Kann man da die Kettenregel anwenden?

Warum setzt du g(t) = f(tx), ändert doch nichts, oder?

Und hast du vielleicht ein einfaches Beispiel, damit es vielleicht etwas klarer wird? :-)

LG

---

1. Ja das ist die Kettenregel

2. x wird nur als Parameter betrachtet

3. Nein, ein leichtes Beispiel habe ich nicht.