Schwimmbecken. Volumen - Füllvorgang

Question

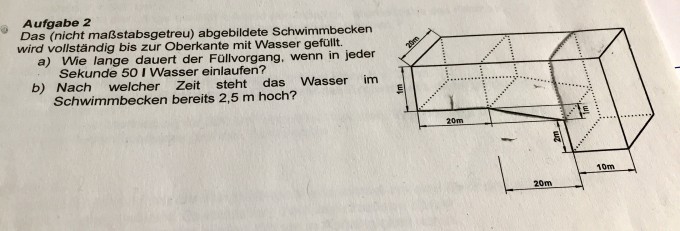
Also ich habe ein paar Fragen zu dieser Aufgabe

Zuallererst habe ich dieses Schwimmbecken in 2 Teile gegliedert (kann man das erkennen & ist das richtig - muss man das so machen)?

Dann muss ich doch sicherlich das Volumen berechnen, rechne ich dann bei beiden "Hälften" das Volumen aus und rechne die beiden Volumenzusammen (plus)?

Ja und dann verstehe ich Aufgabe a &b auch überhaupt nicht...

Wäre wirklich super nett wenn mir das jemand "verständlich" erklären würde!

:)

Comments

Hallo :-)

Du kannst das Becken in so viele Teile aufteilen, wie Du möchtest.
Hauptsache das Volumen ist am Ende richtig berechnet.
Wenn Du das Volumen ausgerechnet hast, kannst Du es in Liter umrechnen,
dann fällt Dir sicherlich Teil a) leicht zu beantworten.

Beste Grüße
gorgar

---

Ich würde das Becken in 3 Teile aufteilen.
Zwei Quader und ein Dreieckprisma.
b) Wie sieht der Wasserspiegel aus, wenn das Wasser
2,5 m hoch steht? Welches Volumen ist dann mit Wasser
gefüllt? Mit dem Volumen kannst Du dann die Zeit berechnen.

Answer 1

Aus dem Bild erkennt man drei verschiedene Körper, deswegen würde ich das Becken in drei Teile zerlegen und einzeln berechnen und dann zusammenzählen.

Das Volumen in Liter durch 50 teilen ergibt die Sekunden bis es voll ist.

Im letzten Teil der Aufgabe muss zuerst das hintere Becken ganz voll laufen dann hast Du 2 Meter Füllhöhe und dann noch 0.5 Meter im schrägen Teil des Beckens. Die Volumen wieder zusammenzählen und durch 50 teilen.

Answer 2

a)

G = 20·1 + 1/2·(1 + 2)·20 + 10·4 = 90 m²

V = 90·20 = 1800 m³ = 1800000 l

t = 1800000 / 50 = 36000 s = 600 min = 10 h

 

b)

G = 1/2·10·0.5 + 10·2.5 = 27.5 m²

V = 27.5·20 = 550 m³ = 550000 l

t = 550000 / 50 = 11000 s = 183.3 min = 3 h 3.3 min

Answer 3

a) Zunächst bezeichnet man die vordere Wand des Schwimmbeckens als Grundfläche G eines Körpers der überall die Höhe h = 20 m hat. dann berechnet man G als Rechteck 1·20=20, Trapez (2+1)/2·20 = 30 und nochmal als Rechteck 4·10 = 40. G=20+30+40 m²= 80 m². Das Volumen des Schwimmbeckens ist dann G·h = 80·20 = 1600 m³. Das sind 1 600 000 Liter. Wenn in der Sekunde 50 l einlaufen, sind das 1 600 000 :50 = 32 000 Sekunden (8std 53 min 20 sec.