Hi,
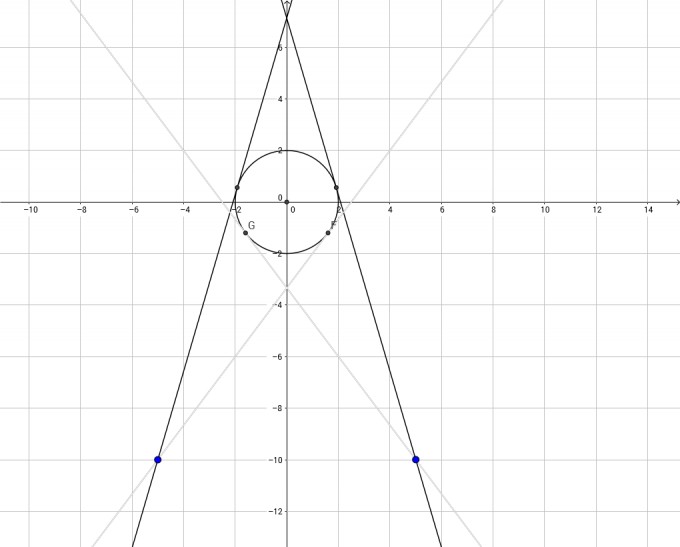
Hier mal ein Skizze. Der blaue Punkt rechts sei A und der Tangentenpunkt dazu (also rechts am Kreis) sei P. Der Mittelpunkt des Kreises ist M.
Es muss gelten: MP*AP = 0, denn die stehen senkrecht aufeinander.
Zudem gilt |MP|^2 = r^2
Für ersteres:
$$PM = \begin{pmatrix} 0\\0 \end{pmatrix} - \begin{pmatrix} x\\y\end{pmatrix} = \begin{pmatrix} -x\\-y \end{pmatrix}$$
$$PA = \begin{pmatrix} 5\\-10 \end{pmatrix} - \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 5-x\\-10-y \end{pmatrix}$$
Mit dem Skalarprodukt von oben:
$$\begin{pmatrix} -x\\-y \end{pmatrix}\cdot \begin{pmatrix} 5-x\\-10-y \end{pmatrix} = 0$$
$$-5x+x^2+10y+y^2 = 0$$
Aus letzterem
$$x^2 + y^2 = 4$$
$$x^2+y^2-4 = 0$$
Gleichsetzen der beiden Bedingungen:
$$-5x+x^2+10y+y^2 = x^2+y^2-4$$
$$y = \frac x2-\frac25$$
Das wieder in die zweite Gleichung einsetzen:
$$x^2-\frac{8}{25}\cdot x-\frac{384}{128} = 0$$
pq-Formel liefert:
$$x_{1} = 1,92$$
$$x_{2} = -1,6$$
Damit wieder in die Geradengleichung:
$$y_{1} = 0,56$$
$$y_{2} = -1,2$$
Die letztere Lösung suchen wir nicht (bei mir im Bild mit G bezeichnet) sondern nur die erstere:
P(1,92|0,56)
Die zweite Lösung (Q) geht genauso, oder man argumentiert über die Symmetrie -> Q = (-1,92|0,56)
Grüße