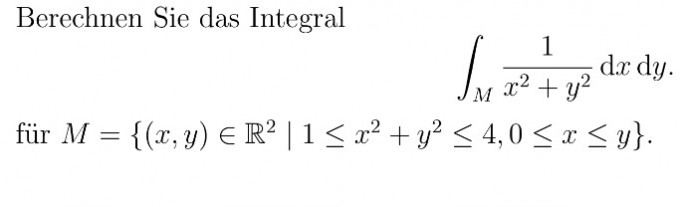Hey:)
Wollt gerade diese Aufgaben machen und dachte, dass die Gleichungen umstellen, es besser ist.
1<=x^2+y^2<=4 <=> 0<= x^2+y^2 -1 <= 3
0<= x<= y
Also hat man einen Kreis mit Mittelpunkt bei (0,-1) mit dem Radius 1.5.
Was fange ich aber mit der zweiten Gleichung an?