ich bin zurzeit am Üben, und beschäftige mich mit dieser Aufgabe: 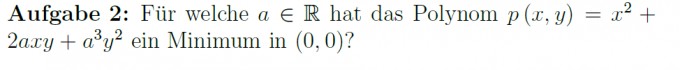
Ich habe hier jetzt mal die partiellen Ableitungen berechnet:
$$ \frac { dp }{ dx } (x,y)=2(x+ay) $$$$ \frac { dp }{ dy } (x,y)=2a(a^2y+x) $$
$$\frac { d^2p }{ dx^2 } (x,y)=2$$$$\frac { d^2p }{ dy^2 } (x,y)=2a^3$$$$\frac { d }{ dx }\frac { dp }{ dy } (x,y)=2a$$
Bei der zweiten partiellen Ableitung nach x, ist die Funktion ja nicht mehr abhängig von a.
Bei der zweiten partiellen Ableitung nach y resultiert. $$\frac { d^2p }{ dy^2 } (x,y)=2a^3$$
Für (0,0) folgt also:
\(\frac { d^2p }{ dy^2 } (0,0)=2a^3\) Für alle \(a > 0 \) würde also ein Minimum resultieren.
Aber ich bin mir da nicht so sicher. Wäre nett falls jemand helfen könnte.
lg
