a)
f(x, y) = (x - 2·y^2 + 3)·(x - 5)
f'(x, y) = [2·x - 2·y^2 - 2, 4·y·(5 - x)] = [0, 0] --> (x = 5 ∧ y = -2) ∨ (x = 5 ∧ y = 2) ∨ (x = 1 ∧ y = 0)
Noch keine Untersuchung mit der Hesse-Matrix. Dies müsste noch gemacht werden. Das überlasse ich dir. Hier noch die Matrix.
f''(x, y) = [2, - 4·y; - 4·y, 4·(5 - x)]
b)
(x - 5)·(x - 2·y^2 + 3) > 0
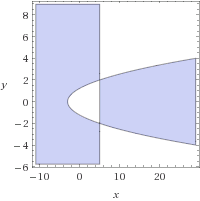
c)
Zeichne die Punkte oben ein. Begründe jetzt wie man eventuell Extrem und Sattelpunkte erkennen kann.