zu 1.) man zeichne den Winkel im Einheitskreis ein. 4-mal das Drittel des Halbkreises (\(=\pi\))
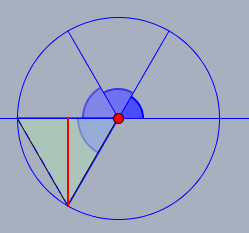
Die rote Strecke ist der \(\sin\). Das ist die Höhe im gleichseitigen Dreieck mit der Seitenlänge 1 - also:
$$\sin{\frac{4\pi}{3}}=-\frac{1}{2}\sqrt{3}$$
zu 2.) ich unterstelle mal, es ist gefragt, was \(\tan{(x-\pi)}\) ist. Man mache sich wieder eine Skizze im Einheitskreis
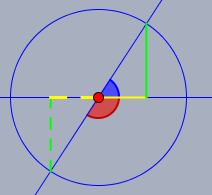
Der blaue Winkel sei \(x\) und der rote \(x-\pi\). Der Tangens dieser Winkel ist jeweils das Verhältnis grüne Strecke zu gelber Strecke - also in beiden Fällen gleich.
$$\tan{(x-\pi)}=\tan{(x)}$$
zu 3.) Zerlege den Term nach der dritten binomischen Formel
$$\sin^4 {(x)} - \cos^4{(x)}=\left( \sin^2 {(x)} - \cos^2{(x)} \right)\left( \sin^2 {(x)} + \cos^2{(x)} \right)$$
Der Faktor mit \(+\) ist =1 - also ist
$$\sin^4 {(x)} - \cos^4{(x)}=\sin^2 {(x)} - \cos^2{(x)} =\left( 1 - \cos^2{(x)} \right) - \cos^2{(x)}\\ \space=1- 2 \cdot \cos^2{(x)}= \frac{1}{2}$$
$$\Rightarrow \cos(x) = \pm\frac{1}{2}$$
und da \(\frac{\pi}{2} < x < \pi\) sein soll, ist \(\cos(x)<0\). Daher gilt hier \(\cos(x)=-\frac{1}{2}\). Und \(\sin(x)\) ist >0 und nach Pythagoras ist \(\sin(x)=\sqrt{1-\cos^2(x)}=\frac{1}{2}\sqrt{3}\)
$$\Rightarrow \sin(x) + \cos(x) = \frac{1}{2}\sqrt{3} - \frac{1}{2}=\frac{\sqrt{3}-1}{2}$$