Gleichung (3x-4)*sin(x) / (x^3 - 10) = cos(x), Lösung in [-5,5]? Nullstellensatz?

Question

 

Zu sagen ist noch, dass die Funktion stetig ist.

Es handelt sich hier um den Nullstellensatz oder?

Ist die Aufgabe so fertig?

Answer 1

Hallo Probe,

ja, es geht um den Nullstellensatz. Dieser hat aber zur Voraussetzung, dass die Funktion innerhalb eines Intervalls definiert und dort stetig ist. Dann hat man mindestens eine Nullstelle, wenn f in diesem Intervall das Vorzeichen wechselt.

Die Funktion  f(x) = (3·x - 4)·SIN(x)/(x^3 - 10) - COS(x)  ist aber für x = ³√10  ≈ 2,15  gar nicht definiert, weil dort der Nenner den Wert 0 hat.

Deswegen nützt dir der Vorzeichenwechsel in [ -1 ; 4 ] nichts, weil der Graph einfach bei x = ³√10  "über die x-Achse springt".

Aber du hast z.B. eine Nullstelle in [ 4 ; 5 ] ⊂ [ -5 ; 5] , 

weil  f(4) ≈ 0,542 > 0   und   f(5) ≈ - 0,375 < 0  gilt. 

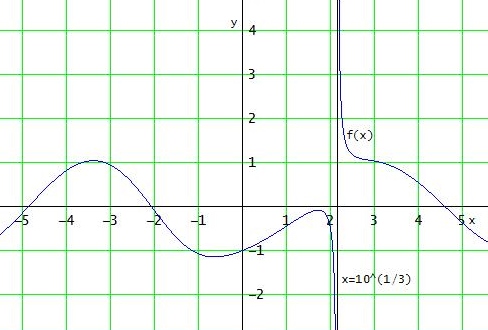
Nullstelle bei  x ≈ 4,6007 ;            [  x ≈  -2,0672  und   x ≈ -4,8602 ]  

Gruß Wolfgang

Comments

                       

---

Du weißt ja:  Immer ....  :-)

---

Hast Du kurz Zeit für eine andere Aufgabe..

---

Um was geht es denn?

---

https://www.mathelounge.de/464792/funktion-f-maximum-minimum

Ich habe die Begründung nicht ganz verstanden.

Gibt kein globales Maximum und Minimum, weil die Funktion gegen +-unendlich strebt?

---

Wenn eine Funktion sowohl beliebig große als auch beliebig kleine Funktionswerte annimmt weil f(x) gegen ±∞ strebt, gibt es doch logischerweise weder einen maximal großen (Maximum) noch einen minimal kleinen (Minimum) Funktionswert. 

---

Vielen Dank für die Hilfe.

Störe ich eigentlich mit den Fragen?

---

Habe ich dir doch schon gesagt: Nette Mädchen stören mich selten :-)

Also nein.