Question

Ist die Folge konvergent oder divergent?

Wie bestimmt man hier den Grenzwert?

Was hat es hier mit dem Summenzeichen auf sich...

Answer 1

Hey probe,

Nutze die Gaußsche Summenformel, diese kannst du, sofern noch nicht geschehen, schnell mit vollständiger Induktion zeigen.

$$ { a }_{ n }=\frac { 1 }{ { n }^{ 2 } } \sum _{ k=1 }^{ n }{ k } =\frac { 1 }{ { n }^{ 2 } } \frac { n(n+1) }{ 2 } =\frac { 1 }{ 2 } \frac { n+1 }{ n } =\frac { 1 }{ 2 } \left( 1+\frac { 1 }{ n }  \right)  $$

Jetzt solltest du bereits sehen, ob die Folge konvergiert.

Gruß

Comments

Sorry, da stand wohl vorher etwas Anderes(?)  Sonst hätte ich gar nicht geantwortet :-)

(Keine Kritik, habe meine Antwort auch editiert. Aber ich hasse Antworten, die genau das gleiche beinhalten :-) )

---

Meinste du meine Antwort oder die Frage? Denn meine Antwort habe ich nachträglich nicht mehr bearbeit.

Lieber drei Antworten mit einheitlichem Ergebnis, als eine Antwort mit drei Ergebnissen ;)

---

"Keine Kritik, habe meine Antwort auch editiert."

Da geht noch was zu editieren.

MfG

Answer 2

Was hat es hier mit dem Summenzeichen auf sich...

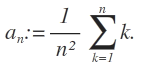Die Summe kannst du einfach mal ausschreiben

a_(n)= 1/n^2 (1 + 2 + 3 + 4 + .... + n) 

1 + 2 + 3 + 4 + .... + n ist eine arithmetische Reihe. Entweder du kennst die Summenformel oder du überlegst dir logisch, was das geben muss. Es gilt:

1 + 2 + 3 + 4 + .... + n = n(n+1)/2 

Daher gilt:

a_(n)= 1/n^2 * (n (n+1))/ 2

Nun die Brüche miteinander multiplizieren, kürzen ... Dann kann man, falls er existiert, den Grenzwert ausrechnen.

a_(n)= 1/n^2 * (n (n+1))/ 2

= (n+1)/(2n) 

=(1 + 1/n)/2 

-----> (1 + 0)/2 = 1/2 

Answer 3

Hallo probe;

die Summe  \(\sum\limits_{k=1}^{n} \) k  hat den Wert  n/2 * (n+1)   

( Summenformel von Gauß,  Standardbeispiel für vollständige Induktion :-) )

Beweis z.B. hier:

http://www.arndt-bruenner.de/mathe/Allgemein/summenformel1.htm

Also gilt:

 a_n  =  1/n²  *  n/2  * (n+1)  =  1/(2n) * (n+1)  =  1/2 + 1/(2n)   hat den Grenzwert  1/2 .

----------------

Weitere Summenformeln:

http://www.arndt-bruenner.de/mathe/Allgemein/summenformel2.htm

Gruß Wolfgang

Comments

"die Summe  ⁿ∑_k=11/k  hat den Wert  n/2 * (n+1) "

Das muss heißen:   ⁿ∑_k=1 k  hat den Wert  n/2 * (n+1)   

MfG

---

Da hast du natürlich recht, danke für den Hinweis.

Dummer Fehler beim Editieren. Habe ihn in der Anwort korrigiert.