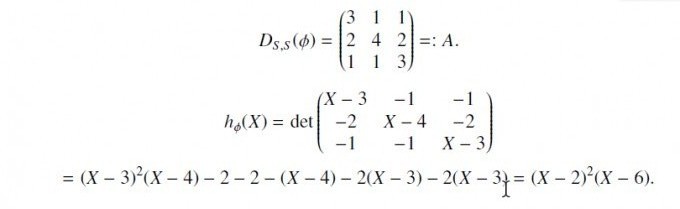Charakteristisches Polynom

Question

Ich weiß grundsätzlich wie man das charakteristische Polynom ausrechnet, jedoch finde ich es manchmal sehr mühsam und frage mich oft, ob es Tricks gibt, wie man schneller das char. Polynom ausrechnen kann.

An sich kommt man ja auf das Ergebnis, wenn man Sarrus oder Laplace anwendet. Dann wendet man Polynomdivision an, oder Pq-Formal um die Nullstellen herauszufinden.

Aber gibt es einen einfacheren Weg, um auf (X - 2)^2(X - 6) zu kommen?

Liebe Grüße

Comments

Warum machen die das in der Musterlösung eigentlich ohne Minus vor dem x^3 ? (An den Eigenwerten ändert sich nichts und faktorisieren muss man ohne das Minus)

Ich hätte auch

χ(x) = -x³ + 10x² - 28x + 24

= -(x^3 - 10x^2 + 28x - 24) 

Beachte. 2^2 * 6 = 24 und 2+2+6 = 10. Damit kannst du (x-2)^2 ( x-6) schon erraten. Nun einfach Klammern auflösen und schauen, ob x^3 - 10x^2 + 28x - 24 herauskommt. 

---

Danke für den Tipp! Ich hoffe in der Klausur bleibt mir dann die Zeit, die Nst.zu erraten bzw. ich hoffe, dass es mir gelingt :D LG

---

Bitte. Wenn in alten Klausuren immer ganze Zahlen herauskommen, sparst du vermutlich Zeit, wenn du die 24 in drei Faktoren zerlegst.

Eine Nullstelle erraten geht meist recht schnell. Sehr oft kommt an Klausuren auch die 1 (plus oder minus) vor. Die sieht man am schnellsten. Auch die 2 siehst du hier recht schnell.

Dann fehlen nur noch 2 Faktoren von 24 . Ansatz 24 = 2* .... * ....

Viel Glück dann!

Answer 1

Wir haben das an der UNI über Sarrus (bei 3 mal 3 Matrix) gelernt , das charakteristische Polynom zu berechnen. Mir ist kein anderer Weg bekannt.

Es sei denn ,Du hast eine Dreiecksmatrix.Dort sind Eigenwerte die Einträge auf der Diagonalen. 

Comments

Ja.. Also bleibt mir nichts anderes übrig als über Sarrus das ganze auszumultiplizieren?

also in die Form  -x^3 + 10x^2 - 28x + 24 bringen polynomdivision (ergibt die Nst. 2)., dann Pq formel um auf die Nst. 2 und 6 zu kommen richtig?

sodass man letztendlich auf (x-2)^2(x-6) kommt.

---

-x³ + 10x² - 28x + 24  habe ich auch erhalten.

x_1.2= 2

x₃=6