ich verzweifle momentan an dieser Textaufgabe:
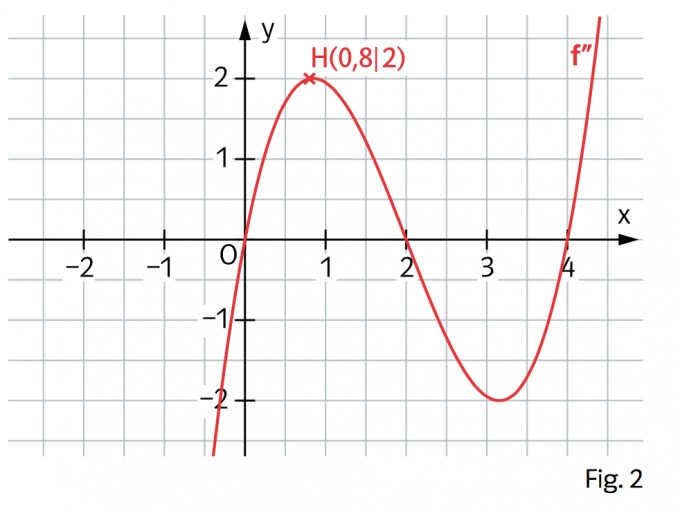
Gegeben ist der Graph der zweiten Ableitungsfunktion f” einer Funktion f (Fig. 2). Welche der folgenden Aussagen sind wahr, welche falsch? Begründen Sie Ihre Antwort.
a) Der Graph von f ist im Bereich –0,3 < x < 2 rechtsgekrümmt.
b) Der Graph von f hat an der Stelle x = 0 einen Sattelpunkt.
c) Der Graph von f ändert an der Stelle x = 0,8 sein Krümmungsverhalten.
Ich habe zwar die Lösungen dafür, jedoch verstehe ich sie nicht bzw. kann den Zusammenfang nicht erkennen:
a) Falsch. Für -0,5 < x < 2 nimmt f"(x) sowohl Werte größer als auch kleiner null an.
b) Falsch. f'(0) muss nicht null sein, das ist aber Voraussetzung für einen Sattelpunkt.
c) Falsch. f" hat an der Stelle x=0,8 ein Maximum, f' hat somit an diser Stelle eine Nullstelle, f ändern sein Krümungsverhalten nicht.
Kann mir bitte jemand das ausführlich erklären, wie ich diese Textaufgabe lösen muss bzw. wie ich vorgehen müsste? Wir haben für solche Aufgaben diese Eselsbrücke(kann leider damit auch nichts anfangen):
Nullpunkt Extrempunkt Wendestelle
f'(x) Nullpunkt Extrempunkt Wendestelle
f"(x) Nullpunkt Extrempunkt Wendestelle
PS: Es soll nicht rechnerich gelöst werden.