Zu a) Ich rate mal ein wenig:
Der Winkel unten rechts (bzw. links), um dessen Größe es ja geht, ist vermutlich mit α bezeichnet. Die Grundseite des gesamten Dachdreiecks besteht aus zwei Strecken die jeweils die Länge a haben und die Dreiecksseite, die das Dach darstellen soll, trägt die Bezeichnung c.
Laut Aufgabenstellung gilt:
a = 6 m , c = 7,8 m
Bestimmt werden soll der Winkel α, der von a und c eingeschlossen wird.
Nun, da es sich um ein rechtwinkliges Dreieck handelt und a die Ankathete des Winkels α und c die Hypotenuse ist, gilt:
cos ( α ) = a / c
und daraus folgt durch Anwendung der Umkehrfunktion der Kosinusfunktion (arccos):
arccos ( cos ( α ) ) = arccos ( a / c )
<=> α = arccos ( a / c )
Werte einsetzen ergibt:
α = arccos ( 6 / 7,8 ) = 39,7 ° (gerundet)
Man könnte auch zunächst die Länge der anderen Kathete (die vermutlich die Bezeichnung b trägt) berechnen, etwa mit dem Satz des Pythagoras:
a ² + b ² = c ²
<=> b ² = c ² - a ²
<=> b = √ ( c ² - a ² )
und dann mit dem arcsin rechnen:
α = arcsin ( b / c ) = arcsin ( √ ( ( c ² - a ² ) / c )
= arcsin ( √ ( ( 7,8 ²- 6 ² ) / 7,8 ) = 39,7 °
und erhält so (natürlich) denselben Wert für die Größe des Winkels α
Zu b) In der folgenden Zeichnung habe ich die auftretenden Winkelgrößen berechnet (rot umrandet):
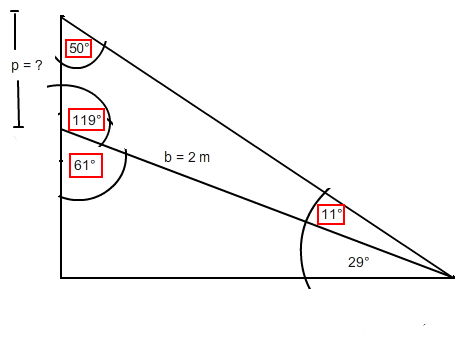
Mache dir klar, dass die Winkel die angegebenen Größen haben müssen.
Die Aufgabe ist nun mit Hilfe des Sinussatzes einfach zu lösen, denn aufgrund dieses Satzes gilt:
p / sin ( 11 ° ) = b / sin ( 50 ° )
[mit b = 2 m gilt:]
<=> p = 2 * sin ( 11 ° ) / sin ( 50 ° ) = 0,498 m