Expotenzielle wachstum / zerfall

Question

Habe probleme mit der aufgabe: Die Höhe einer Pflanze zur Zeit t kann näherunsweise durch eine Funktion f mit f(t)=a+be^-0,536; t >_ 0 , beschrieben werden. Dabei ist t die Zeit in Wochne seit dem Beginn der Beobachtung und f(t) die Höhe in meter. Zu Beginn der Beobachtung war die Pflanze 0,62 meter hoch. Nach 5 Wochen hat sie eine höhe von 1,09 m. a)Bestimme a und b und zeichne Schaubild f. b) Wie hoch kann die pflanze maximal werden. Kann mir wer die aufgabe komplett lösen ? denke dann kann ich sie nachvollziehen

Comments

bauche weiterhin hilfe

---

Bin gern bereit weitere Auskünfte
über meine Antwort zu geben.

Answer 1

f(0)=0,62 daher           (1) a+b=0,62

F(5)=1,09 daher a+b·e-2,28=1,09 oder (2) a+0,07b=1,09

(1) und (2) sind zwei Gleichungen mit zwei Unbekannten.

Comments

ähm leider versteh ich deine antowrt nicht. kannst du es bitte etwas genauer ausführen XD am besten komplett. zb wo hast du die -2,28 her usw. Hilfe :P Brauch am besten wirklich die komplette lösung da ich es so wirklich nicht versteh

---

Siehe Antwort von Georgborn.

Answer 2

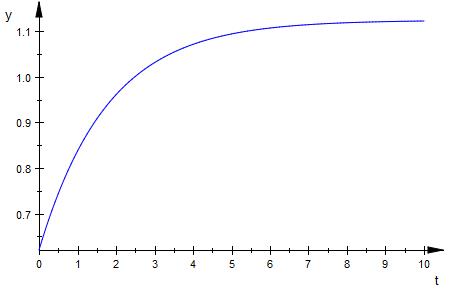
f ( t ) = a + b*e^{-0.536*t}
( 0 | 0.62 )
( 5 | 1.09 )

f ( 0 ) = a + b * e^{-0.536*0} = 0.62
a + b *1 = 0.62
a + b = 0.62

f ( 5 ) = a + b * e^{-0.536*5} = 1.09
a + b * 0.06856 = 1.09

a + b = 0.62
a + b * 0.06856 = 1.09  | abziehen
----------------------------
b * 0.93144 = -0.47

b = -0.5046

a + b = 0.62
a - 0.5046 = 0.62
a = 1.1246

f ( t ) = 1.1246 - 0.5046 * e^{-0.563*t}

Wie hoch kann die Pflanze höchstens
werden.

f ( t ) = 1.1246 - 0.5046 * e^{-0.563*t}
t = ∞
f ( t ) = 1.1246 - 0.5046 * e^{-0.563*∞}
f ( t ) = 1.1246 - 0
f ( t ) = 1.1246  m