Bild einer Funktion bestimmen

Question

Wie bestimmt man das Bild von f?

z.B. f(x)=-1+cos(x²)

f(]-√x,√x[)=?

Comments

Was stellst du dir denn unter dem "Intervall" ]-√x,√x[ vor?

---

Dort ist die Funktion f gegeben.     

Answer 1

Hallo probe,

a)   Bild_f   =  [-2 ; 0]     , weil  -1 ≤ cos(x²)  ≤  1

b) macht so keinen Sinn   x müsste eine Zahl sein oder anders heißen

Gruß Wolfgang

Comments

Wie geht das bei 1+sin(x²), für das selbe Intervall?

---

Bild_f = [ 0 ; 2 ]      ,    1+(-1) ≤  f(x)  ≤  1 + 1

---

Die Lösung soll [1,2] sein.

---

Das wäre bei   1 + sin²(x)  der  Fall, wegen  0  ≤  sin²(x) ≤ 1

---

Sicher? mhhhh steht so in der Lösung.

Wie bestimmt man denn das Bild allgemein?

---

> Sicher? mhhhh steht so in der Lösung.

Ja:

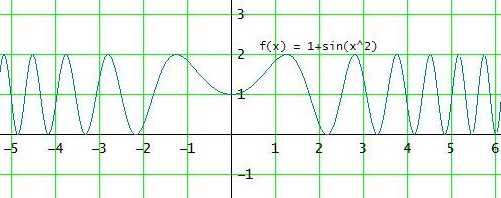
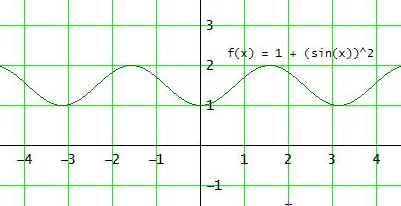
> Wie bestimmt man denn das Bild allgemein? 

Überblick über den Graph verschaffen:

Lim_x→± ∞ f(x)   [ oder gegen die Randstellen von D ]  , Grenzwerte an den Definitionslücken , Extrempunkte bestimmen.

Gedanklich alle Punkte des Graphen auf die y-Achse projizieren.

Alle Werte, die diu dort triffst, gehören zum Bild

---

Mir ist das jetzt klar.

Wie mache ich das, wenn ich keinen Taschenrechner habe und wenig Zeit zur Verfügung....?
Gibt es einen einfach Trick..?

---

Einen allgemeinen einfachen Trick gibt es nicht.

Das geht dann nur bei "übersichtlichen" Funktionstermen, wo man - wie oben - den Verlauf zumindest von Teiltermen kennt.

P.S.

Das Mehrfachdrücken des Daumens (in meiner History 10-mal :-) )  bringt nichts, es bleibt immer 1 Punkt. :-)

---

Wieso, bekommt man dafür denn keine Punkte?

---

Es gibt nur einen Pluspunkt für "gute Antwort" durch die Fragestellerin. Andere Leser(innen) können weitere "Daumen" vergeben.

und immer .... , aber das weißt du ja :-)

---

Wolfgang,

vielleicht kannst Du mir hier https://www.mathelounge.de/475604/wie-bestimme-ich-ein-globales-minimum-maximum helfen, ich schreibe bald meine Prüfung... Vielleicht kannst Du eine Funktion nehmen, die sowohl globale als auch lokale Punkte hat. Dann könntest Du mir ausführlich erklären wie man die globalen bestimmt. Lokale Extrempunkte bestimmen, kann ich..

Falls Du keine Zeit hast oder nicht willst, ist auch nicht schlimm....

Answer 2

Ok, das ist richtig. Unter der Annahme , dass im Intervall x als Parameter gilt kannst du dann auch das Bild bestimmen. Nenne also x=a. Es ist f(0)=0 und f(√a)=-1+cos(a)

Solange a∈[0,π], dann ist das Bild [0,-1+cos(a)].

Ist a>π, so ist das Bild [0,-2]

Answer 3

Da x jede Zahl sein kann ist ]-√x,√x[  jedes offene Intervall.

Man kann Nullstellen und Extrema bestimmen. Außerdem sollte man die Achsensymmetrie des Graphen berücksichtigen. Im Intervall [-2,  2] ist (0|0) Hochpunkt und die Tiefpunkte sind ungefähr bei (-1,8|-2) und (1,8|-2).

Comments

Da x jede Zahl sein kann

Ach so?! Wie ist es mit negativen x?

---

Dann ist das Intervall komplex.

---

Was ist denn ein komplexes Intervall?

---

Das ist hier ein Intervall auf der imaginären Achse der Gaußschen Zahlenebene.