Hi mathemaggie! :-)
f(0) = 1
f'(0) = 2
f''(0) = 2
f'''(0) = 3
P1,0(x) = f(0) + f'(0)·x = 1 + 2x
P2,0(x) = f(0) + f'(0)·x + f''(0)·x^2/2! = 1 + 2x + x^2
P3,0(x) = f(0) + f'(0)·x + f''(0)·x^2/2! + f'''(0)·x^3/3! = 1 + 2x + x^2 + 1/2·x^3
x ∈ [-1, 1)
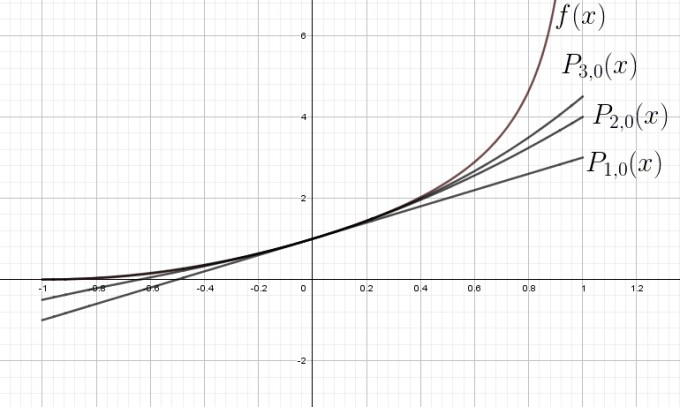
Man sieht, wie sich die Graphen der Taylorpolynome mit steigendem Grad f nähern.
f(x) = Pn,a(x) + Rn,a(x)
Rn,a(x) = f(x) - Pn,a(x)
Δy = Rn,a(x) = f(x) - Pn,a(x)
y = f(x)
Δy / y = (f(x) - Pn,a(x)) / f(x)
n = 2, a = 0, x = 0,5
Δy / y = (f(0,5) - P2,0(0,5)) / f(0,5)
Δy / y = (2,405 - 2,25) / (2,405) ≈ 0,06 = 6%
Beste Grüße
gorgar