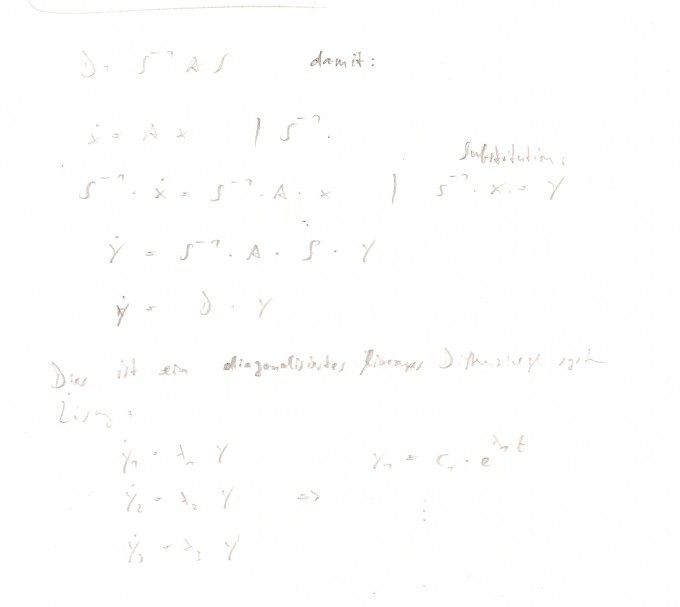Linear homogenes DGL System AWP lösen

Question

Hallo könnte mir jemand erklärend folgende Aufgabe vorrechnen? 

Danke

Answer 1

Hallo if1888, die Matrix dieses Differenzialgleichungssystems lautet
-1 0 1
0 -1 1
1 1 -3
Bitte berechne im ersten Schritt die Eigenwerte und Eigenvektoren dieser Matrix.  Wenn du dazu Fragen hast, frag ruhig.  Wenn du damit fertig bist, helfe ich dir weiter.

Comments

Und wie gehts weiter.

Habe folgende 3 Ew 

X1=((-√3+1)/2, (-√3+1)/2, 1)^T *C

X2=((√3+1)/2, (√3+1)/2, 1)^T *C

X3=(-1, 1, 0)*a

Noch eine Frage, wie sind Sie auf die Matrix gekommen?

---

Hallo Rokko, das Differenzialgleichungssystem kann man umschreiben zu
(x1_Punkt)     (-1 0 1)    (x1)
(x2_Punkt) =  (0 -1 1) * (x2)
(x3_Punkt)     (1 1 -3)    (x3)

=> x_Punkt = A * x   mit x_Punkt und x Vektoren, A Matrix

Jetzt zu den Eigenwerten.  Welche Eigenwerte hast du?  Das, was du geschrieben hast, sind *Eigenvektoren*, und die sind korrekt.

Es gilt, siehe Wikipedia „Diagonalisierung“,
D = S^-1 * A * S,
wobei S eine Matrix ist, die aus v1 bis v3 zusammengesetzt ist.  D ist eine Diagonalmatrix mit den Eigenwerten.  Überzeuge dich mit dem Taschenrechner, dass das korrekt ist.

Weiter siehe Bilder.

---

Ich kann leider das 1. Bild nicht erkennen..

---

Hallo Rokko, alles klar.  Ich bin eigentlich ein Formeleditor-Verweigerer, aber ich verstehe dich.  Ich probiere es mal so, ohne Formeleditor, aber wenigstens getippt statt handschriftlich:
Es gilt x_Punkt = A * x   |   S^-1 *
S^-1 * x_Punkt = S^-1 * A * x   |   Substitution S^-1 * x = y
y_Punkt = S^-1 * A * S * y   |   Wikipedia “Diagonalisierung”:  D = S^-1 * A * S
y_Punkt = D * y
D ist die Diagonalmatrix mit den Eigenwerten von A.  Wir haben jetzt ein diagonalisiertes lineares Differenzialgleichungssystem.  Aufgeteilt in einzelne skalare Gleichungen:
y1 = lambda1 * y
y2 = lambda2 * y
y3 = lambda3 * y
Lösung :
y1 = c1 * exp(lambda1 * t)
y2 = c2 * exp(lambda2 * t)
y3 = c3 * exp(lambda3 * t)
Hast du noch Fragen ?

---

Das Ganze jetzt mit dem Formeleditor:
$$ \dot { x } =A\cdot x\quad |\quad { S }^{ -1 }\cdot  $$
$$ { S }^{ -1 }\cdot \dot { x } ={ S }^{ -1 }\cdot A\cdot x\quad |\quad Substitution\quad { S }^{ -1 }\cdot x=y $$
Boah, das mit dem Formeleditor dauert Stunden.  Mach ich nur, wenn du mit dem Anderen nicht klar kommst.  Dann gib mir bitte Bescheid.

Answer 2

habs auch mal gerechnet:

Comments

Und wie gehts weiter?