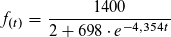Wachstum-Funktion ermitteln können.

Question

Wie muss man hier vorgehen?

Anna und Berta besuchen eine höhere Schule mit 700 Schülerinnen. Aus Langeweile setzen die beiden ein Gerücht in die Welt. Zu Beginn kennen nur 2 Personen das Gerücht. Das Gerücht verbreitet sich allerdings schnell und so kennen es nach einem Tag bereits 128 Schülerinnen.

Ermittle die Wachstumsfunktion, wenn man davon ausgeht, dass sich das Gerücht nach einem logistischen Modell G(t) verbreitet.

Answer 1

Eine allgemeine Formel für ein logistisches Wachstumsmodell ist

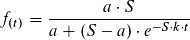
dabei steht

S für die Schranke/Endhöhe, in diesem Fall 700 Schüler

a = f(0) = Anfangswert = Schnittpunkt mit y-Achse, hier sind es zu Beginn 2 Personen, die das Gerücht kennen

t = Zeit

k gilt es herauszufinden mithilfe der Information, dass nach einem Tag (t = 1) 128 Personen (f₍₁₎= 128) das Gerücht kennen.

Die bekannten Werte in die Formel eingesetzt ergibt



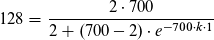
Mit einigen Umformungen kannst du dann k ermitteln, in diesem Fall = -4,354. Falls du dazu Fragen hast, bitte melden.

Somit ergibt sich die Funktion

Answer 2

f(x) = g/(1 + (g/a - 1)·b^x)

Wir wissen aufgrund der Bedingungen

f(∞) = g = 700

(0) = a = 2

f(1) = 128 --> b = 143/11168

Damit lautet die Funktion

f(x) = 700/(1 + (700/2 - 1)·(143/11168)^x) 

oder näherungsweise

f(x) = 700/(1 + 349·0.012804^x)

Comments

Wie bist du auf 143/11168 gekommen? :/

---

f(1) = 128 aufstellen a und g einsetzen und nach b auflösen.

f(1) = 700/(1 + (700/2 - 1)·b^1) = 128