Schreiben Sie die Folge (an) rekursiv in der Form .... Grenzwert bestimmen.

Question

Sei a_n = sin(sin(sin(...sin 1))) n ∈ ℕ

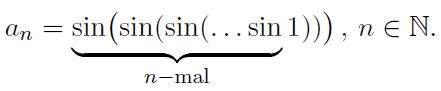
Schreiben Sie die Folge (a_n) rekursiv in der Form a_n = f(a_n-1), n ∈ ℕ, mit a₀ = 1.

Begründen Sie mit aus der Schule bekannten Eigenschaften von sin x, dass die Zahlenfolge monoton und beschränkt ist, und bestimmen Sie den somit existierenden Grenzwert.

Komme mit dieser Aufgabe leider nicht zurecht und wäre dankbar für eure Hilfe. :)

Answer 1

Rekursion: a₁=sin1; a_n=sin(a_n-1)

Grenzwert: 0

Comments

Habe dieselbe Aufgabe:
Das mit der Rekursion klingt sehr einleuchtend, aber könntest du bitte erklären, wie du auf den Grenzwert 0 kommst? :)

---

Wenn 0<x<π dann ist sinx>sin(sinx)>0 (Das Lot vom Ende des Bogens im Einheitskreis ist kleiner als der Bogen).. Die Folge ist streng monoton fallend und nach unten durch 0 beschränkt.

---

Die Folge ist streng monoton fallend und nach unten durch 0 beschränkt.
Daraus folgt nicht, dass der Grenzwert gleich Null ist.

---

Nein, nur wenn 0 größte untere Schranke ist.

---

Ich vergaß zu erwähnen, dass 0 größte untere Schranke ist