Hallo Letra,
Sattelpunkt (1|1) = Wendepunkt mit waagrechter Tangente
Das ergibt drei Bedingungen:
f(1) = 1 , denn S liegt auf dem Graph
f '(1) = 0 , denn Tangente in x=1 hat die Steigung 0
f "(1) = 0 , S ist Wendepunkt
3 Bedingungen → 3 Unbekannte sind festgelegt
Punktsymmetrie zu O → nur ungerade Exponenten von x
die "ganzrationale Funktion kleinstmöglichen Grades" hat also die Form
f(x) = ax5 + bx3 + cx
f '(x) = 5ax4 + 3bx2 + c
f "(x) = 20ax3 + 6bx
f(1) = 1 → a + b + c = 1 G1
f '(1) = 0 → 5·a + 3·b + c = 0 G2
f "(1) = 0 → 20·a + 6·b = 0 G3
Subtrahiere: G2 - G1 , dann fällt c weg und du erhältst zusammen mit G3 ein lineares GS mit den Unbekannten a und b, das du wohl lösen kannst.
Einsetzen von a und b in G1 ergibt dann c.
Kontrolllösung: a = 3/8 ; b = - 5/4 ; c = 15/8
f(x) = 3/8 · x5 - 5/4 · x3 + 15/8 · x
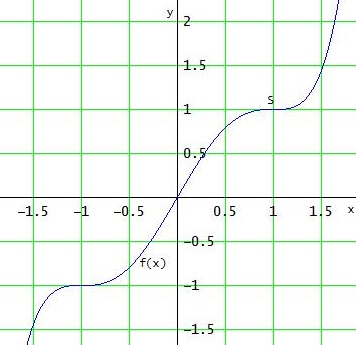
------------
Mit diesem Online-Rechner kannst du Steckbriefaufgaben lösen (selbstverständlich nur zur Kontrolle :-))
http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm
Gruß Wolfgang