Skizzen:
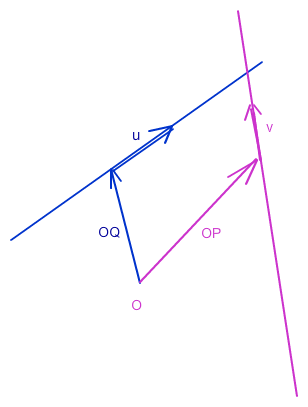
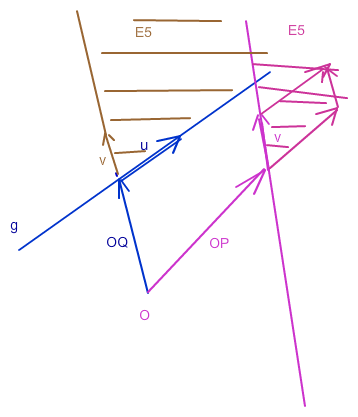
Es ist ja nicht selbsverständlich, dass die beiden Geraden überhaupt in einer Ebene liegen. Um das zu prüfen, könntest du den Schnittpunkt ausrechnen.
Deine Fragestellung setzt das aber schon voraus. Da die beiden Richtungsvektoren nicht parallel zueinander sind, spannen sie die Ebene E5 auf und alle Punkte beider Geraden liegen in E5. Für die Parametergleichung von E5 kannst du deshalb einfach einen Punkt auf g oder h nehmen und die beiden Richtungsvektoren dort anhängen.(2. Bild) .