Bestimme die Wendepunkte und die Krümmungsbereiche f. 2) bestimme die Wendetangente der Funktion

Question

 Hallo

Die Aufgabe steht bereits oben.

Ich soll die Wendepunkte und die krümmungsbereiche zuerst bestimmen.

Danach auch die Wendetangene

Meine Funktion lautet

f(x)=1/13(x^4+4x^3-18x^2)

Wie geht nun der Vorgang um die Lösung zu bekommen.

Vielen Dank !!

Lg

Answer 1

Hallo Lisa,

f(x) = 1/13 · (x⁴ + 4x³ - 18x²) 

f '(x) = 4/13 · (x³ + 3·x² - 9x) 

f "(x) = 12/13 · (x² + 2·x - 3)

f "(x) = 0   ⇔  x² + 2·x - 3 = 0  ⇔ (x - 1)·(x + 3) = 0   →  x₁ = 1 ;  x₂ = - 3 

Der Term der nach oben geöffneten Parabel ist zwischen den Nullstellen negativ, also

f "(x) <  0 in  ] - 3 ; 1 [    →   Rechtskrümmung  in  [ -3 ; 1 ]

f "(x)  >  0   in  ] - ∞ ; -3 [  und  in  ] 1 ; ∞ [  

                                      →   Linksskrümmung in  ] - ∞ ; -3 ]  und  in  [ 1 ; ∞ [  

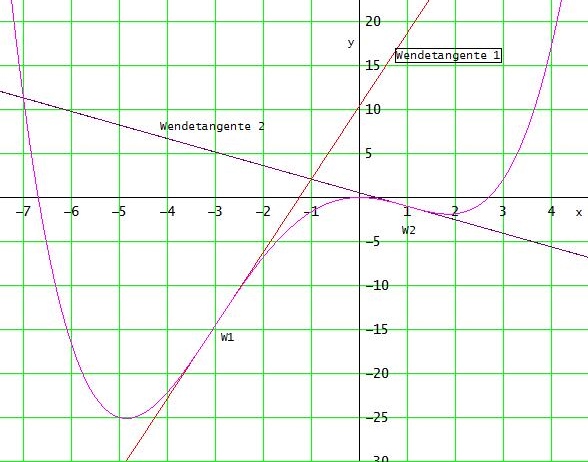
Wendepunkte: W₁ (-3 | -189/13 )   und  W₂ ( 1 | -1 ) 

Wendetangenten:

y = f ' (x_w) * (x - x_w) + y_w   

t₁ :  y = 108/13 * (x + 3) -189/13  = 27/13 * (4x + 5)  ≈  8,31·x + 10.38  

t₂ :  y = - 20/13 * (x - 1) - 1  =  1/13 * ( -20x + 7)  ≈ - 1.54·x + 0.54  

Gruß Wolfgang