Größtmögliche Dreieck in einer Fläche bestimmen

Question

f(x) = 5/6    x³    -     10/3     x²       +    3x

 

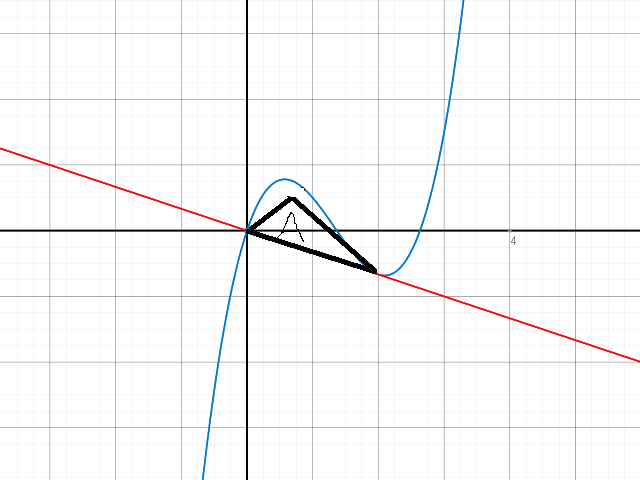
Nun wird eine Fläche durch f  und der Tangente t(x) = -1/3  x    .begrenzt   (siehe Skizze ) !

 

∫₀²   ( f(x) - t(x)  )  dx    =  10/9           hab ich schon alles berechnet ........

Nun zur Frage ........ Bestimme unter allen Dreiecken, die innerhalb der Fläche, die die Tangente mit dem Graphen von f einschließt liegen, dasjenige mit dem größten Flächeninhalt !

 

Meine erste Idee war, dass man vielleicht die strecke a schon setzt mit (0/0)  zum Berührungspunkt  B(2;  -2/3) ..... und foglich noch c auf f legt oder irgendwie so

 

Danke für eure Hilfe

 

Answer 1

Ich würde die rote Gerade so parallel verschieben, dass sei die blaue Kurve berührt.

Dazu müsste man erst mal feststellen für welchen x-Wert die blaue Kurve die Steigung -1/3 hat.

Danach den y-Wert dieses Punktes berechnen. Genügt dir das als Anfang?

Comments

dann hast du ja aber genau einen punkt .... du musst aber doch eine funktion für A aufstellen um mit differenzieren auf A_max zu kommen ?

---

Moment! Ich sehe das Problem.

B kann gar keine Ecke des Dreiecks sein, da die Seite, die dort nach oben weggehen sollte automatisch ausserhalb des Dreiecks zu liegen kommt.

---

Kanntst Du schon mit Vektoren rechnen?

---

Hier die Skizze, mit der man vielleicht arbeiten sollte:

Beantworte noch JR's Frage. Damit man weiss, was man benutzen kann.