Aufgabe 1:
Zeichne den Graphen der Funktion \( f(x)=-\frac{1}{2} x+2 \) in das gegebene Koordinatensystem und berechne \( \int \limits_{-1}^{6}\left(-\frac{1}{2} x+2\right) d x \)
Aufgabe 2:
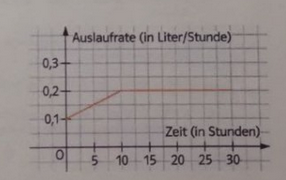
Aus einem bis an den Rand gefüllten 15-Liter-Eimer láuft nach folgendem Schaubild Wasser aus einem Loch im Boden aus. Berechne, wie viel Liter Wasser sich nach 25 Stunden noch im Eimer befinden.
Autgabe 3
In einem Pumpspeicherwerk wird nachts Wasser aus einem unteren Becken in ein oberes Speicherbecken gepumpt. Zur Stromerzeugung kann das Wasser am Tag über eine Turbine wieder abgelassen werden. Zwischen 2.00 und 5.00 Uhr werden folgende Messungen (alle 15 Minuten) fur die einlaufende Wassermenge ins Speicherbecken aufgezeichnet:
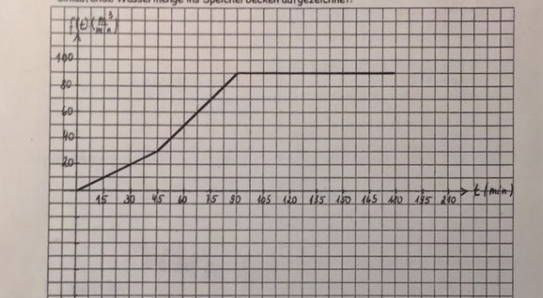
a) Bestimme rechnerisch die gesamte Wassermenge, die zwischen 2.00 und 5.00 Uhr einfließt?
b) \( A b \) 5. 00 Uhr fließen \( 60 \mathrm{m}^{2} / \mathrm{min} \) gleichmäßig ab. Zeichne diesen "Ablauf" in das Koordinatensystem ein.
c) Berechne nach welcher Zeit das Speicherbecken wieder geleert ist?
d) Berechne \( \int \limits_{0}^{210} f(t) d t \). Gib an, welchen Größenwert dieses Integral in der oben angegebenen Anwendungssituation wiedergibt.
Ich schreibe nächste Woche eine Matheklausur zum Thema Integral. Das ist eine Probeklausur die wir zum üben bekommen haben (Klausur vom parallel Kurs). Ich habe die aufgaben soweit ich konnte bearbeitet und wollte wissen, ob die so richtig sind.
Hilfsmittelfreier Teil:
1) A= 1/2 • (2+5)•6 = 21 FE ?
2) 1/2•(15+25)•0,2=4 15l-4-=11l → Es befinden sich nach 25h noch 11Liter im Tank. ?
Mit GTR:
3a) ADreieck = 1/2•45•30=675
ATrapez= 1/2•(30+90)•45=2700
ARechteck=90•90=8100
AGesamt= 675+2700+8100=11475m3 ?
b) wie zeichnet man das ein ? Das verstehe ich nicht ganz ?
c) muss man da einfach das Ergebnis durch 60 teilen ? also : 11475 ÷ 60= 191,25 ??
d) Verstehe ich auch nicht wirklich.. weiß nicht wie ich da vorgehen soll
Vielen Dank schonmal für eure Hilfe ! Es wäre mir wirklich wichtig !