Es wird die Zeit und der Ort für den
möglichen Zusammprall berechnet.
Ausgehend von deiner Skizze ist für das Schiff
( x | y )
v ( Schiff) = 4.167 m/s
( 80 | 4.167 * t )
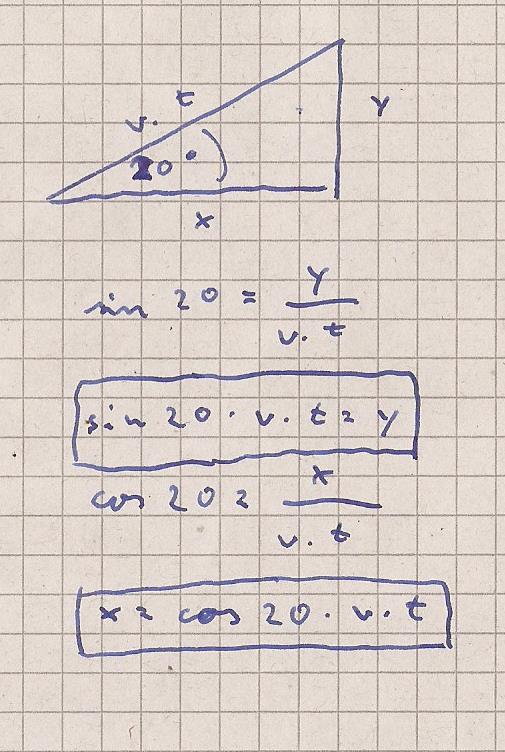
Das Streckendreick für die Fähre sieht wie folgt
aus
α = 20 °
t : die Zeit bis zum Zusammenprall ist für beide
Schiffe gleich
Es gilt :
y Koordinate Schiff = y-Koordinate Fähre
4.167 * t = sin ( 20 ) * v * t + 50 m
x Koordinate Schiff = x-Koordinate Fähre
80 m = cos ( 20 ) * v * t + 1 m
4.167 * t = sin ( 20 ) * v * t + 50 m
80 m = cos ( 20 ) * v * t + 1 m
2 Gleichungen mi 2 Unbekannten
t = 18.9 sec
v ( Fähre ) = 4.45 m/s
In allen anderen Fällen kommt es nicht zur Kollision.