"Was fehlt ist nun ein geeigneter Startwert um x1 berechnen zu können. Es darf hierfür ein x0 fast frei gewählt werden. Es sollte allerdings darauf geachtet werden, dass ein Startwert gewählt wird, der in der Nähe der interessanten Nullstelle zu finden ist." (-Unknown, Matheartikel)
Ich habe eine Frage bezüglich des Newtonverfahrens. Beim herumspielen ist mir folgendes Aufgefallen:
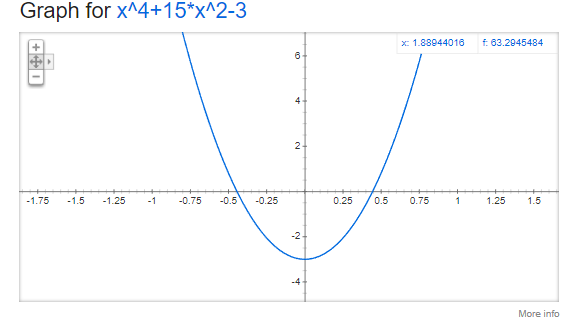
f(x)=x^4+15x^2-3 -----> f(x)= 4x^2+30x
Habe mir jetzt -1 als Startwert genommen, ist zwar nicht der naheliegenste aber nicht unglaublich weit weg.
f(-1)=(-1)^4+32*(-1)^2-3= 28
f'(-1)=4*(-1)^2+30*(-1)= -26
x1= -1-(28/-26) = 2.076923 → falsch
Was habe ich falsch gemacht?